#Calculando P(X < 28) em uma N(25,36)
pnorm(q = 28,
mean = 25,
sd = sqrt(36))[1] 0.6914625O R oferece funcionalidades para manipular distribuições de probabilidades. Para cada distribuição, existem quatro operações fundamentais representadas pelas letras:
d - calcula a densidade de probabilidade de f(x) no ponto.
p - calcula a função de probabilidade acumulada F(x) no ponto.
q - calcula o quantil correspondente a uma dada probabilidade.
r - sorteia uma amostra aleatória da distribuição.
Para melhor entendermos as quatro operações, vamos considerar que \(X∼N(\mu = 25,\sigma^2 = 36)\), \(Y∼Poisson( \lambda = 8)\) e \(Z∼Gama(\alpha= 1,\beta = 5)\).
Suponha que queiramos determinar \(P(X<28)\). Para calcular esta probabilidade, utilizaremos a função pnorm.
Principais argumentos da função pnorm:
q - o quantil da distribuição Normal que desejamos obter a área abaixo dele;
mean - a média da distribuição;
sd - o desvio padrão da distribuição.
#Calculando P(X < 28) em uma N(25,36)
pnorm(q = 28,
mean = 25,
sd = sqrt(36))[1] 0.6914625Atenção para evitar confusões: é necessário especificar o desvio padrão ao utilizar a função pnorm (bem como nas demais funções p, q e r - norm).
Suponha que desejamos obter uma amostra aleatória de tamanho 10 de uma normal padrão.
Principais argumentos da função rnorm :
n - o número de valores que desejamos gerar da distribuição Normal;
mean - a média da distribuição;
sd - o desvio padrão da distribuição.
#Obtendo uma amostra aleatória de tamanho 10 de uma N(0,1)
rnorm(n = 10) [1] -0.24159253 0.80033200 -0.82379949 0.24253012 -1.49269336 1.36599720
[7] 1.00432487 0.07024207 -0.48147790 0.77799177Não informamos os parâmteros da normal em rnorm neste caso, pois são os valores pré-definidos da função.
E se desejarmos obter uma amostra aleatória de \(X\) de tamanho 10?
#Obtendo uma amostra aleatória de tamanho 10 de uma N(25,36)
rnorm(n = 10,
mean = 25,
sd = 6) [1] 32.36889 32.55645 39.42981 22.55276 21.18927 32.76447 24.47216 27.62307
[9] 18.82635 21.23760Qual o valor do 3o decil de \(X\)?
Principais argumentos da função qnorm:
p - a probabilidade abaixo do quantil da distribuição Normal que desejamos obter;
mean - a média da distribuição;
sd - o desvio padrão da distribuição.
#Obtendo o 3o decil de uma N(25,36)
qnorm(p = 0.3,
mean = 25,
sd = 6)[1] 21.8536Qual o valor de \(f(10)\)?
Principais argumentos da função dnorm:
x - o valor no qual deseja avaliar o valor da função densidade de probabilidade da distribuição Normal;
mean - a média da distribuição;
sd - o desvio padrão da distribuição.
#Calculando f(10) em uma N(25,36)
dnorm(x = 10,
mean = 25,
sd = sqrt(36))[1] 0.002921383Qual a probabilidade de \(Y\) ser igual a 10?
Principais argumentos da função dpois:
x - o valor no qual deseja avaliar o valor da função densidade de probabilidade da distribuição Poisson;
lambda - a média da distribuição de Poisson.
#Calculando P(Y = 4) se Y ~ Poisson(8).
#P(Y = 4) = f(4) em distribuições discretas
dpois(x = 10,
lambda = 8)[1] 0.09926153Qual a probabilidade de \(Y\) ser menor do que 4?
Principais argumentos da função ppois:
q - o quantil da distribuição Poisson que desejamos obter a área abaixo dele;
lambda - a média da distribuição Poisson.
#Calculando P(Y < 4) se Y ~ Poisson(8).
ppois(q = 3,
lambda = 8)[1] 0.04238011que é equivalente a…
#Somando P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
sum(dpois(x = 0:3,
lambda = 8))[1] 0.04238011Qual a probabilidade de \(Z\) ser menor do que 0,5?
Principais argumentos da função pgamma:
q - o quantil da distribuição Gama que desejamos obter a área abaixo dele;
shape - parâmetro de forma da gama;
rate - parâmtero de escala da gama.
Neste caso, seja \(X∼Gama(a, r)\), consideramos a forma da distribuição gama dada por \[f_X(x)=\frac{1}{s^aΓ(a)}x^{a−1}e^{−rx},x>0 \quad a,b>0\]
#Calculando P(Z > 0.5) se Z ~ Gama(1,5).
pgamma(q = 0.5,
shape = 1,
rate = 5,
lower.tail = FALSE)[1] 0.082085A modificação do argumento lower.tail para FALSE faz com que seja calculado o complementar da distribuição acumulada, isto é, é calculado \[P(Z>0,5)=1−P(Z\leq0,5)=1−P(Z<0,5)=1−F_Z(0,5)\]
A segunda igualdade é justificada pois \(Z\) é uma variável contínua.
Atividade: Calcule o que se pede:
\(P(23<X<30)\)
\(P(3<Y<30)\)
Gere uma amostra de uma distribuição \(F\) com 2 e 4 graus de liberdade;
Qual o valor de \(c\), tal que \(P(Z>c)=0,7\);
Plotando a função densidade de probabilidade de uma distribuição normal com média 10 e variância 25. Usaremos do ggplot2 o stat_function.
Principais argumentos da função stat_function:
fun - a função a ser plotada;
args - os valores dos argmentos que a função definifa em fun depende (tem que ser definidos em uma lista).
# Ativando pacotes
library(ggplot2)
library(tibble)
#Plotando o gráfico da densidade de uma N(10,25)
ggplot(data = tibble(z = c(-10,30)),
mapping = aes(x = z)) +
stat_function(fun = dnorm,
args = list(mean = 10,
sd = 5)) +
labs(y = "Densidade") +
theme_minimal()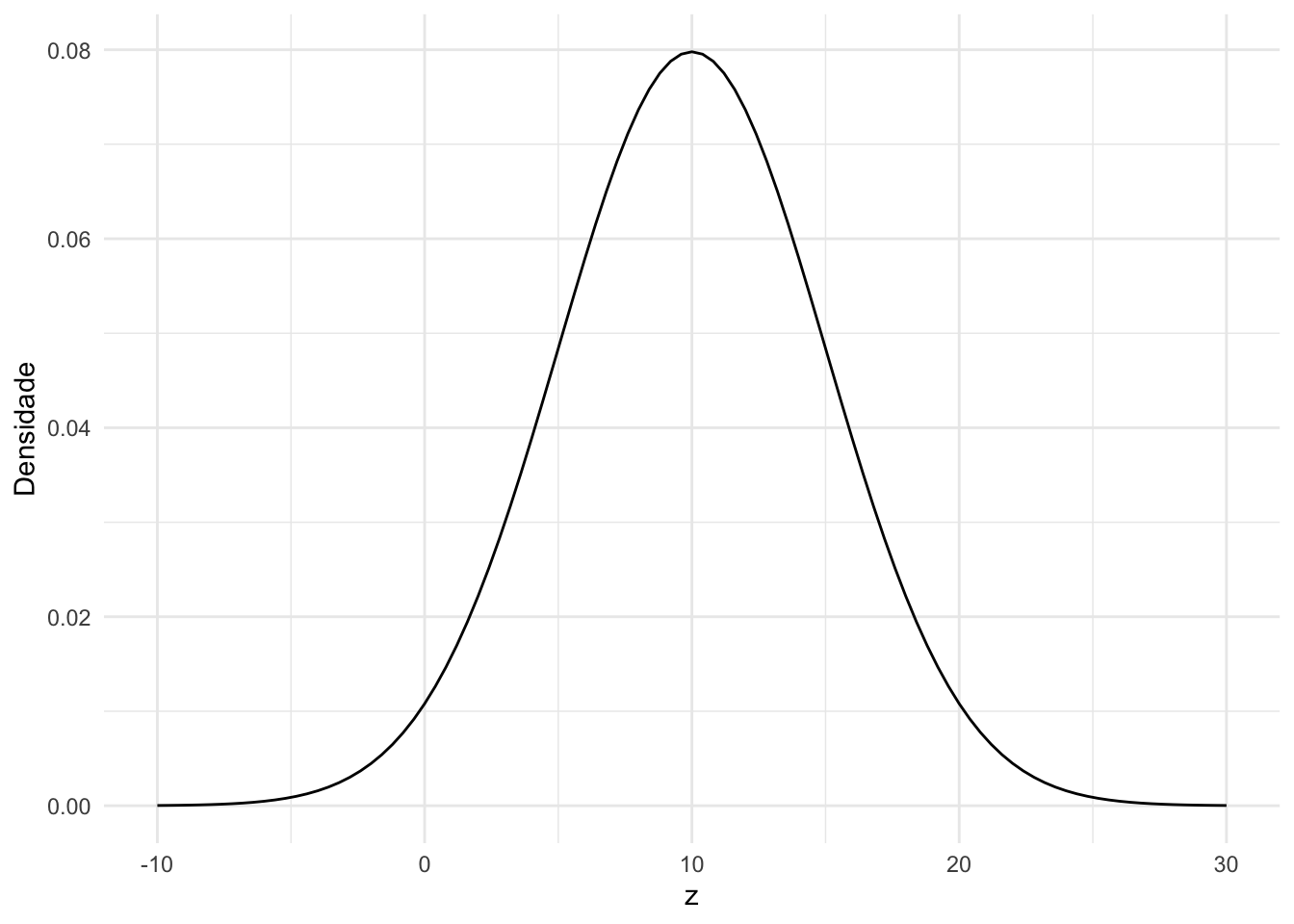
Plotando a função de distribuição acumulada de uma distribuição normal com média 10 e variância 25.
#Plotando o gráfico da função de distribuição acumulada de uma N(10,25)
ggplot(data = tibble(z = c(-10,30)),
mapping = aes(x = z)) +
stat_function(fun = pnorm,
args = list(mean = 10,
sd = 5)) +
labs(y = "Distribuição acumulada") +
theme_minimal()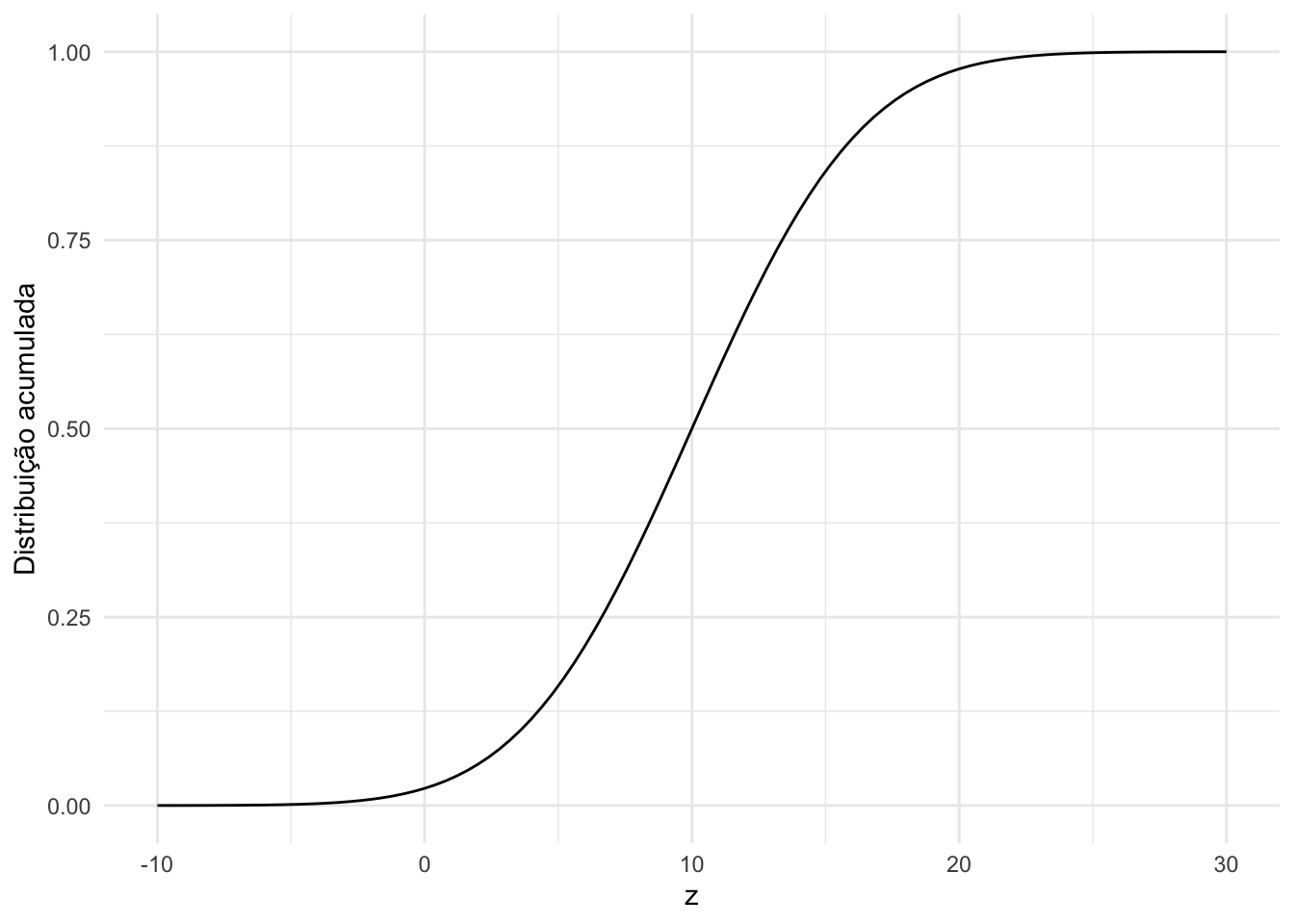
Gerando uma amostra aleatória de uma N(10,25). Em seguida, suponha que não conhecemos s distribuição e gostaríamos de checar se a amostra tem um formato semelhante com a distribuição N(10,25).
#Gerando uma amostra de tamanho 300 de uma N(10,25)
base = tibble(amostra = rnorm(300,10,5))
#Plotando o histograma da amostra com base na frequênica
#Controlando as amplitudes dos intervalos de classe
hist1 = base |>
ggplot(mapping = aes(x = amostra)) +
geom_histogram(binwidth = 3,
fill = "Blue") +
labs(y = "Frequência") +
theme_minimal()
#Plotando o histograma da amostra com base na frequênica
#Controlando o número de intervalos de classe
hist2 = base |>
ggplot(mapping = aes(x = amostra)) +
geom_histogram(bins = 7,
fill = "Blue") +
labs(y = "Frequência") +
theme_minimal()
# Ativando pacote
library(patchwork)
#Plotando dois gráficos em uma mesma figura
hist1 + hist2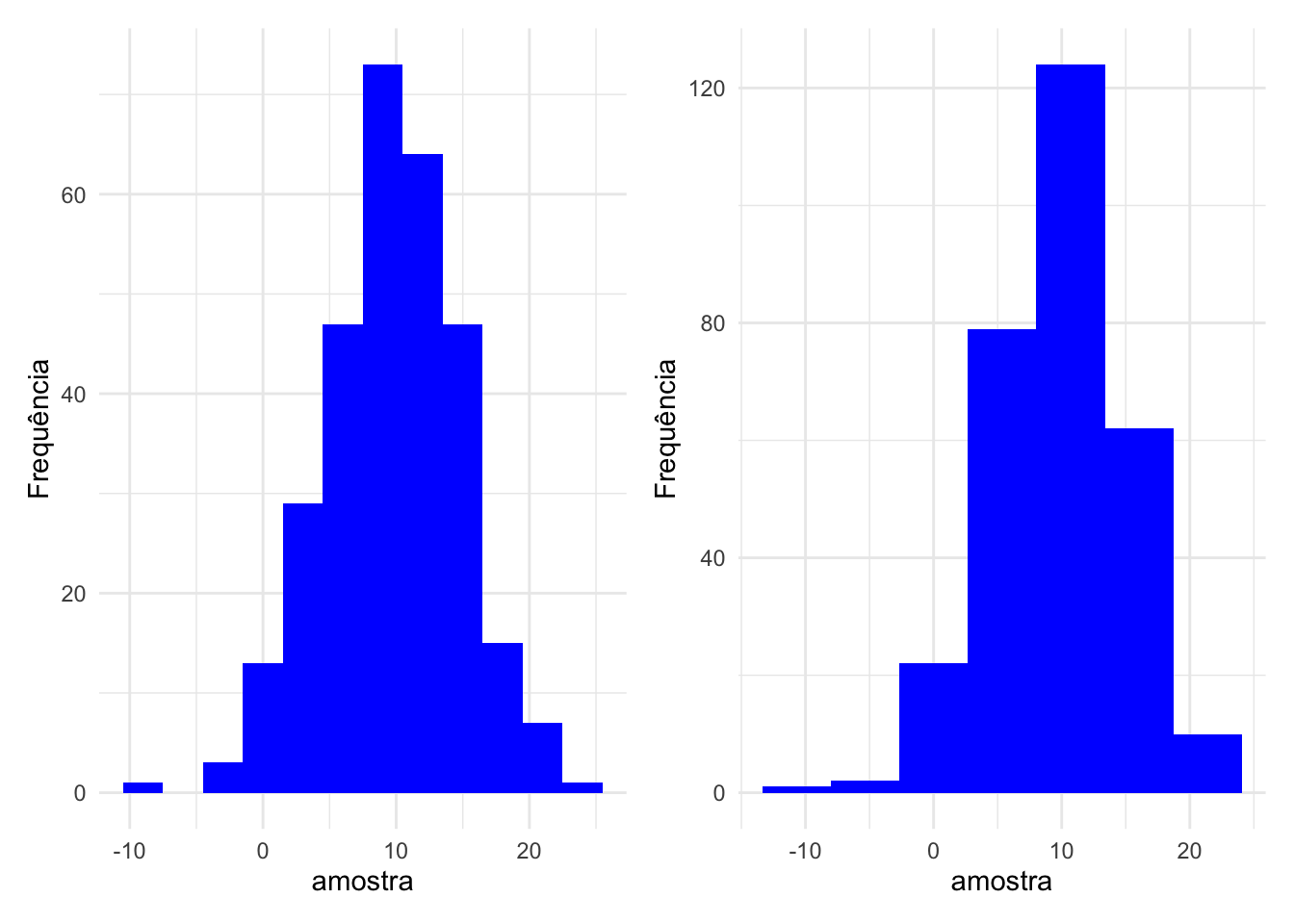
O argumento binwidth determina o tamanho dos intervalos desejados para o histograma. Em vez de especificar o tamanho do intervalo, você pode definir o número de intervalos através do argumento bins. É possível notar as discrepâncias entre o número de intervalos de classe dos dois histogramas mencionados: o primeiro possui 11 intervalos, enquanto o segundo possui 7.
Para comparar o histograma com a densidade de uma distribuição, é necessário que o histograma não seja baseado nas frequências. Para realizar essa alteração, adicionaremos o argumento y dentro de aes no geom_histogram.
#Plotando o histograma da amostra com base na frequênica
hist_freq = base |>
ggplot(mapping = aes(x = amostra)) +
geom_histogram(binwidth = 3) +
stat_function(fun = dnorm,
args = list(mean = 10,
sd = 5),
colour = "Red") +
labs(y = "Frequência") +
theme_minimal()
#Plotando o histograma da amostra com base na densidade
hist_dens = base |>
ggplot(mapping = aes(x = amostra)) +
geom_histogram(mapping = aes(y = after_stat(density)),
binwidth = 3) +
stat_function(fun = dnorm,
args = list(mean = 10,
sd = 5),
colour = "Red") +
labs(y = "Densidade") +
theme_minimal()
hist_freq + hist_dens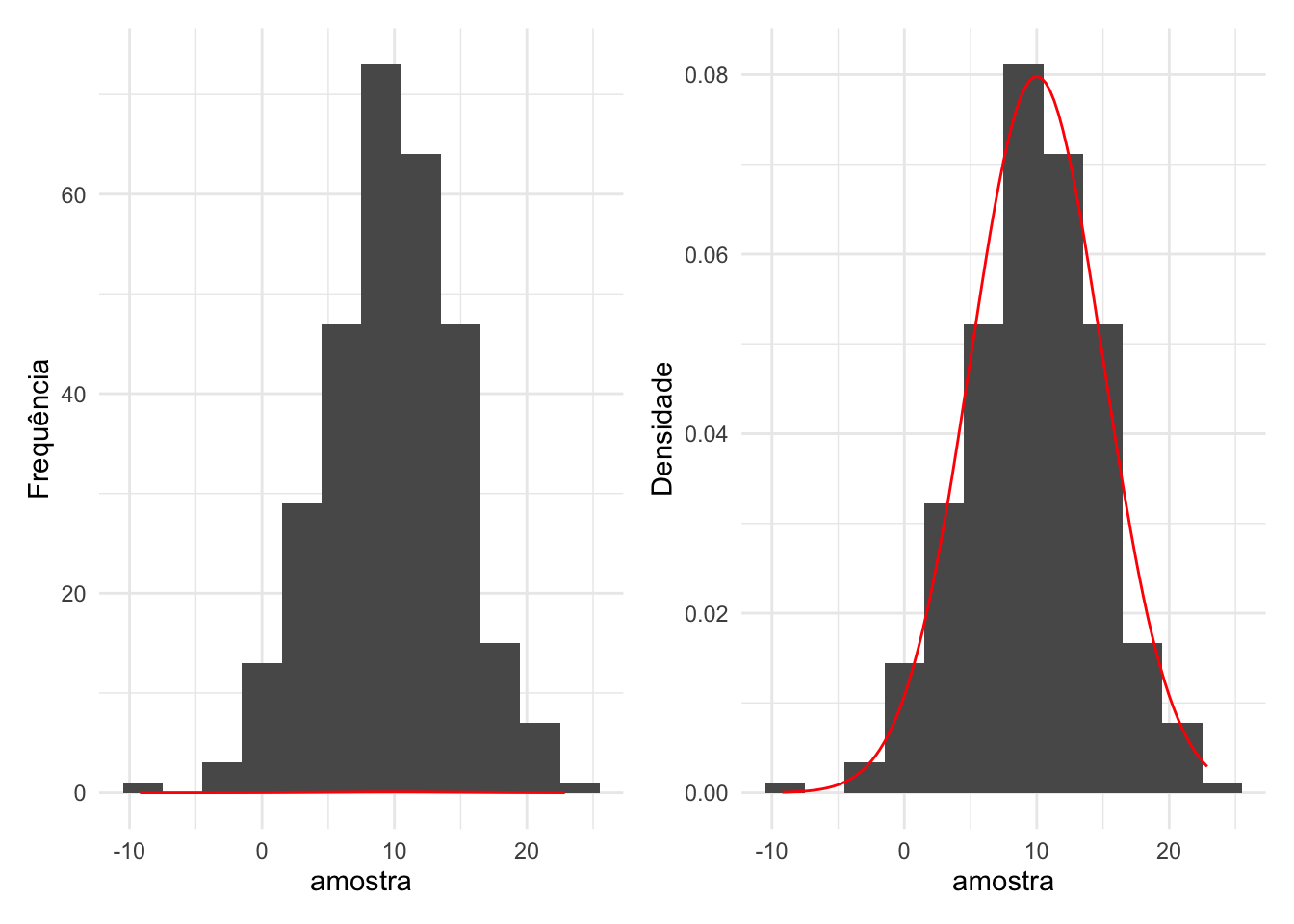
Se desejarmos plotar uma função de probabilidade ao invés de uma função densidade de probabilidade. Basta fazermos as adequações no stat_function. Suponha que \(V \sim Poisson(\lambda = 1)\). Vamos plotar o gráfico da função de probabilidade para \(v = 0, 1, \ldots, 10\).
#Plotando o gráfico da função probabilidade de uma Poisson(1)
ggplot(data = tibble(x = 0:10),
mapping = aes(x = x)) +
stat_function(geom = "point",
n = 11,
fun = dpois,
args=list(lambda = 1),
colour = "Red") +
labs(x = "v",
y = "P(V = v)") +
scale_x_continuous(breaks = seq(0, 10, 1)) +
theme_minimal()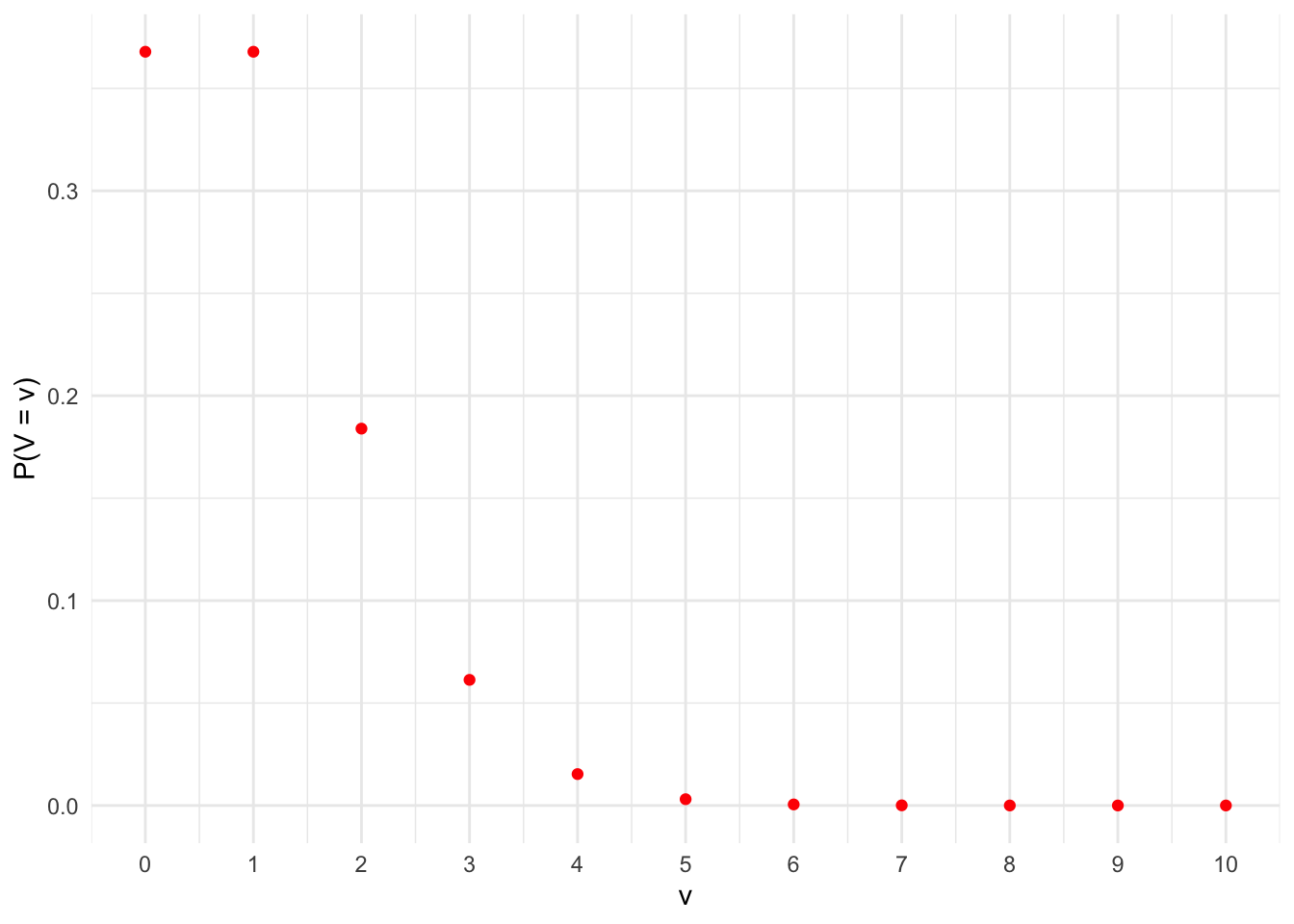
Os argumentos geom e n permitem que seja feito um gráfico de pontos na quantidade de pontos especificado (11 pois de 0 a 10 existem 11 números inteiros).
Outras distribuições:
dexp - densidade da exponencial;
rchisq - sorteia uma amostra da distribuição qui-quadrado;
qt - calcula o quantil de uma t-student;
pf - calcula F(x) de uma F;
rbeta - sorteia uma amostra da distribuição beta;
dunif - densidade de uma uniforme (contínua);
E a uniforme discreta???