#Definindo os elementos da nossa população
pop = c(2,6,6,7,10)10 Distribuições Amostrais
Entendemos que o desafio da inferência estatística consiste em estabelecer conclusões acerca dos parâmetros populacionais a partir de uma amostra coletada.
Considere o cenário a seguir:
Populacão: Indivíduos com 18 anos ou mais residentes no bairro do Ingá.
Variável de interesse será: \(X\) - renda dos residentes do Ingá com idade superior a 18 anos.
Parâmtero de interesse: \(\mu\) - renda média dos residentes do Ingá com idade acima de 18 anos.
Estatística: \(\bar{X}\) - a renda média amostral dos residentes do Ingá com idade igual ou superior a 18 anos.
Imagine que uma Amostra Aleatória Simples (AAS) de \(n\) elementos tenha sido coletada. A partir disso, conseguimos determinar um valor específico para \(\bar{X}\), denominado \(\bar{x}_1\). Com base nesse valor, realizaremos inferências sobre \(\mu\).
Se coletarmos uma segunda amostra, também com tamanho \(n\), é altamente provável que a nova média amostral, que chamaremos de \(\bar{x}_2\), seja diferente da primeira, ou seja,\[\bar{x}_1 \neq \bar{x}_2.\]
Entender o comportamento da estatística \(\bar{X}\), ao retirar diversas amostras de mesmo tamanho, conforme o plano amostral estabelecido, é essencial para realizar inferências sobre o parâmetro de interesse \(\mu\). Para alcançar essa compreensão, é necessário analisar a distribuição amostral da estatística \(\bar{X}\). Como obter essa distribuição?
A seguir, estabeleceremos um procedimento para obter a distribuição amostral de algumas estatísticas e também verificar empiricamente alguns dos conceitos teóricos abordados na disciplina de GET00182 - Estatística II. Vamos iniciar essa discussão pela média amostral.
10.1 Distribuição Amostral da Média
Para começar, suponhamos uma população composta por N = 5 indivíduos, com os valores da variável de interesse especificados a seguir.
Assumindo que o plano de amostragem adotado é Amostragem Aleatória Simples (AAS) com reposição, serão coletadas amostras de tamanho 2.
#Vamos definir o tamanho da amostra com a qual iremos trabalhar
n = 2Agora, procederemos à coleta de 1.000 amostras de tamanho n = 2 armazenando-as em uma matriz. Para isso, utilizaremos a função sample.
Principais argumentos da função sample :
- x - o vetor com os valores a ser sorteado;
- size - o número de elementos que serão sorteados;
- replace - devem ser consideradas retiradas com reposição?
#Vamos definir o número de vezes que uma amostra de tamanho 2 será sorteada.
num.amostra = 1000
#Definindo uma matriz com 1000 colunas e 2 linhas preenchida com NA
mat.amostras = matrix(data = NA,
ncol = num.amostra,
nrow = n)
#Sorteando 1.000 amostras de tamanho 2 e armazenando cada amostra sorteada em uma coluna da matriz mat.amostras
for(i in 1:num.amostra){
mat.amostras[,i] = sample(x = pop,
size = n,
replace = TRUE)
}O objeto mat.amostras contem 1.000 amostras de tamanho 2. Neste contexto, cada coluna da matriz representa uma amostra de tamanho 2 selecionada aleatoriamente da população de interesse. Independentemente da estimativa de interesse, a estatística correspondente será calculada para cada amostra, ou seja, para cada coluna. Portanto, num.amostra representa o tamanho da amostra da estatística que estará disponível para análise.
Posteriormente, calcularemos a média amostral para cada uma das 1.000 amostras de tamanho 2 selecionadas. Isso equivale a determinar a média de cada coluna da matriz. Para realizar esse cálculo, utilizaremos a função apply.
Principais argumentos da função apply :
- X - uma matriz ou um array;
- MARGIN - um valor que vai indicar se a operação será executada sob as linhas (1) ou sob as colunas (2);
- FUN - a função que será aplicada.
#Calcular a média para cada coluna da matriz
media.amostral = apply(X = mat.amostras,
MARGIN = 2,
FUN = mean)Para analisarmos o comportamento das estimativas obtidas, podemos representar as médias amostrais observadas por meio de um histograma.
#Ativando pacotes
library(tibble)
library(ggplot2)
#Visualizar o histograma das médias amostrais
ggplot(data = tibble(valores = media.amostral),
mapping = aes(x = valores)) +
geom_histogram() +
labs(x = expression(bar(x)),
y = "Frequência",
title = "n = 2")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.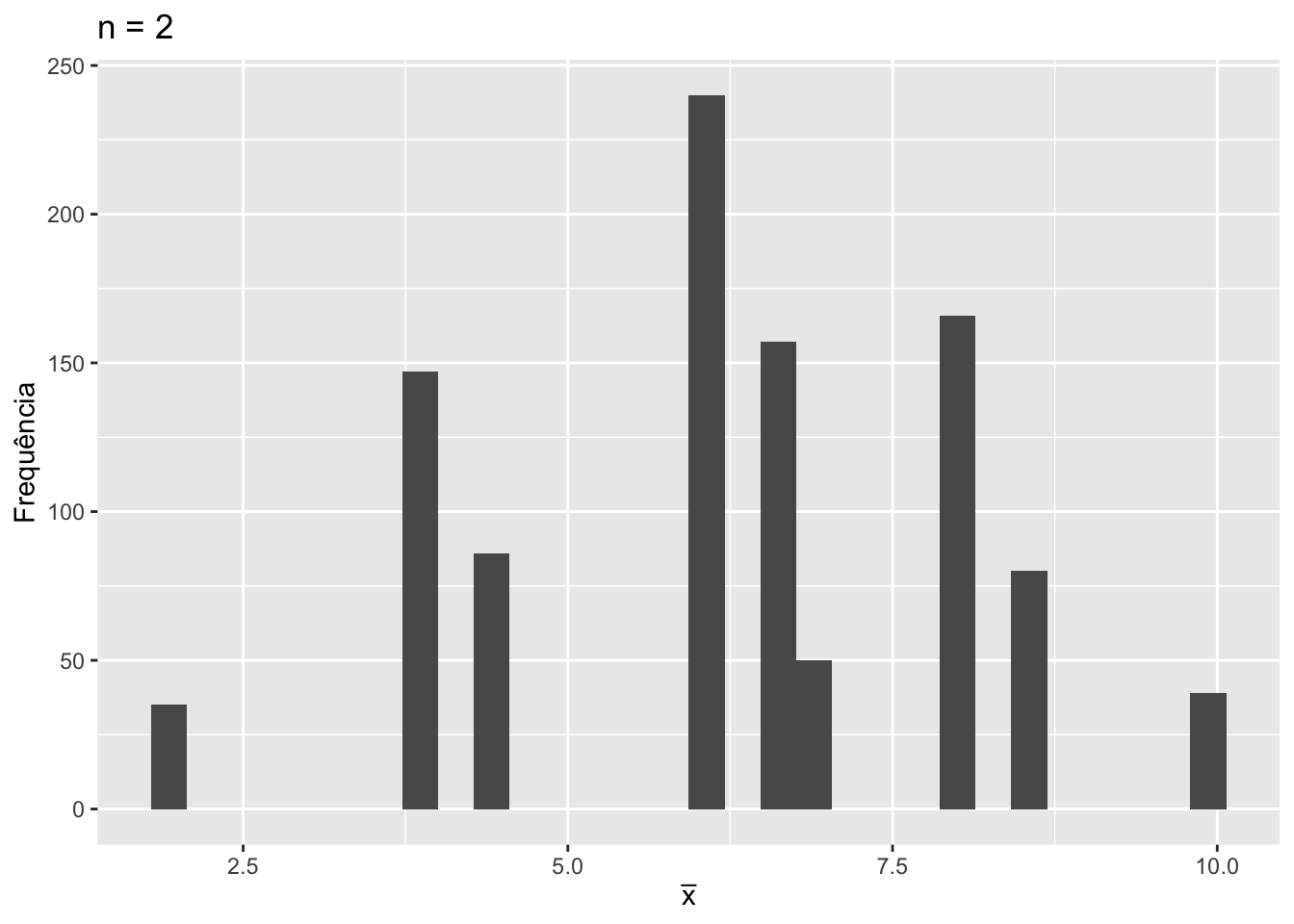
Nota-se que a distribuição amostral apresenta valores concentrados, com probabilidades mais elevadas para valores próximos de 4.
Como essa distribuição se comportaria se utilizássemos um tamanho de amostra maior do que \(n = 2\)? Para explorar essa questão, repetiremos o procedimento considerando \(n = 20\)!
#Vamos definir o tamanho da amostra que iremos trabalhar
n = 20
#Vamos definir o número de vezes que uma amostra de tamanho 20 será sorteada
num.amostra = 1000
#Definindo uma matriz com 1000 colunas e 20 linhas preenchida com NA
mat.amostras = matrix(data = NA,
ncol = num.amostra,
nrow = n)
#Sorteando 1.000 amostras de tamanho 20 e armazenando cada amostra sorteada em uma coluna da matriz mat.amostras
for(i in 1:num.amostra){
mat.amostras[,i] = sample(x = pop,
size = n,
replace = TRUE)
}
#Calcular a média para cada coluna da matriz
media.amostral = apply(X = mat.amostras,
MARGIN = 2,
FUN = mean)
#Visualizar o histograma das médias amostrais
ggplot(data = tibble(valores = media.amostral),
mapping = aes(x = valores)) +
geom_histogram(bins = 15) +
labs(x = expression(bar(x)),
y = "Frequência",
title = "n = 20")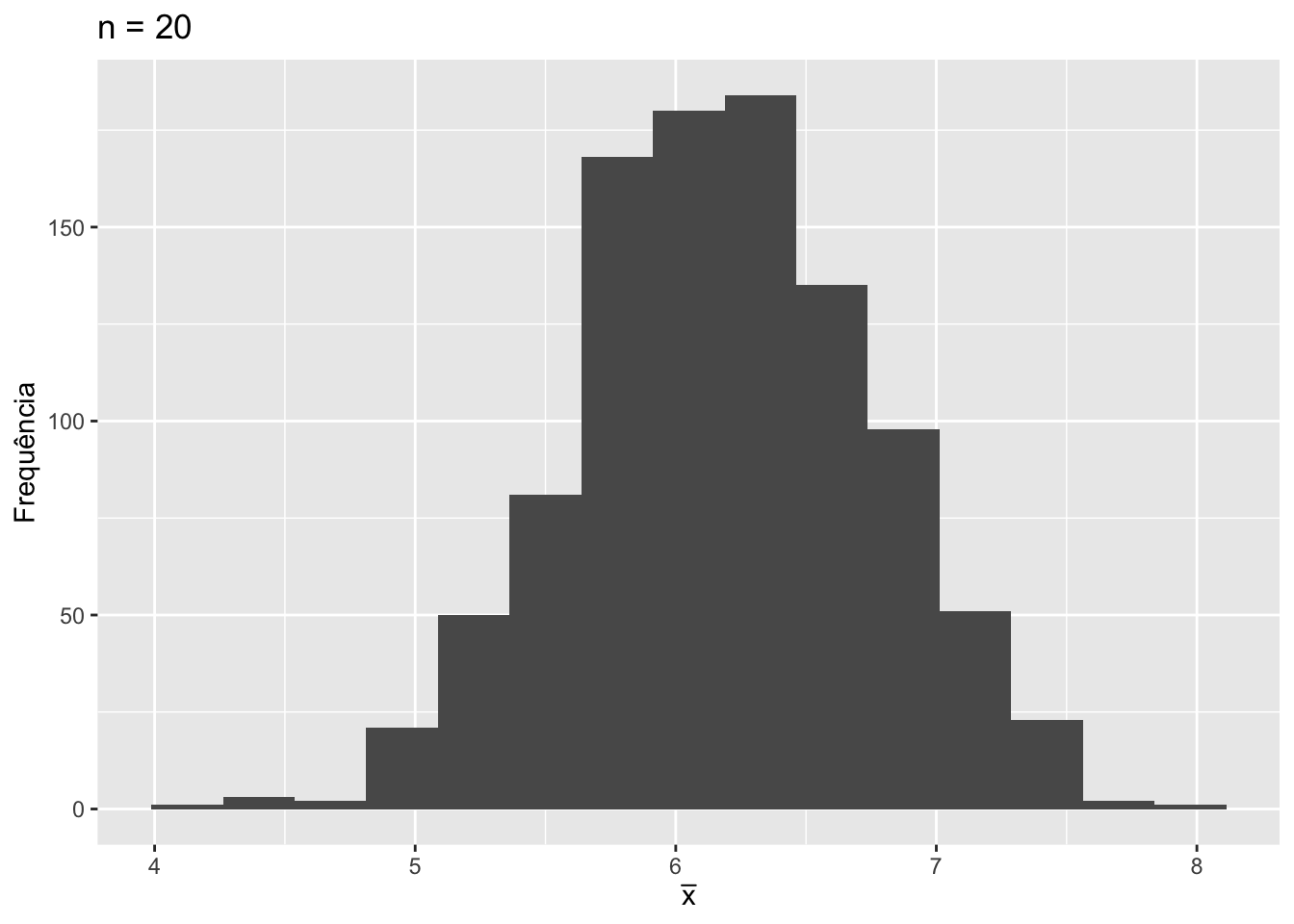
Ao aumentarmos o tamanho da amostra de \(n = 2\) para \(n = 20\), como se alterou o formato da distribuição amostral de \(\bar{X}\)?
O histograma mostrado acima representa o comportamento da distribuição de probabilidade de \(\bar{X}\). Estamos familiarizados com essa distribuição? A seguir, apresentaremos um resultado que estabelece a distribuição da estatística da média amostral.
10.1.1 Teorema do Limite Central (TCL)
A pergunta levantada na seção anterior, sobre qual seria a distribuição da média amostral, pode ser respondida pelo TLC.
Para uma amostra aleatória simples de tamanho \(n\), denotada por \((X_1,\ldots,X_n)\), extraída de uma população com média \(\mu\) e variância finita \(\sigma^2\), a distribuição amostral da média \(\bar{X}\) se aproxima de uma distribuição normal com média \(\mu\) e variância \(\sigma^2/n\), à medida que n cresce, ou seja, \[\bar{X} \sim N\left(\mu,\frac{\sigma^2}{n}\right).\]
Para verificar empiricamente o teorema, vamos analisar a distribuição amostral de \(\bar{X}\) para diferentes tamanhos de amostras, especificamente (n = 3, 4, 20 e 200).
#Vamos calcular a média populacional
med.pop = mean(pop)
#Vamos calcular a variância populacional
#Note que não usamos a função var, pois ela calcula a variância amostral
var.pop = 1/(5) * ((1-med.pop)^2 + (3-med.pop)^2 + (5-med.pop)^2 - (5-med.pop)^2 + (7-med.pop)^2)
# -------------------- Executando para n = 3 ---------------------
#Vamos definir o tamanho da amostra que iremos trabalhar
n = 3
#Vamos definir o número de vezes que uma amostra de tamanho n será sorteada
num.amostra = 1000
#Definindo uma matriz com 1000 colunas e 3 linhas preenchida com NA
mat.amostras = matrix(data = NA,
ncol = num.amostra,
nrow = n)
#Sorteando 1.000 amostras de tamanho 3 e armazenando-as nas colunas da matriz mat.amostras
for(i in 1:num.amostra){
mat.amostras[,i] = sample(x = pop,
size = n,
replace = TRUE)
}
#Calcular a média para cada coluna de mat.amostras
media.amostral = apply(X = mat.amostras,
MARGIN = 2,
FUN = mean)
#Visualizar o histograma das médias amostrais e comparar com a densidade da distribuição Normal indicado pelo TLC
graf1 = ggplot(data = tibble(valores = media.amostral),
mapping = aes(x = valores)) +
geom_histogram(aes(y = after_stat(density)),
bins = 15) +
stat_function(fun = dnorm,
args = list(mean = med.pop,
sd = sqrt(var.pop/n)),
colour = "Red") +
labs(x = expression(bar(x)),
y = "Densidade",
title = "n = 3")
# -------------------- Executando para n = 4 ---------------------
#Vamos definir o tamanho da amostra que iremos trabalhar
n = 4
#Vamos definir o número de vezes que uma amostra de tamanho n será sorteada
num.amostra = 1000
#Definindo uma matriz com 1000 colunas e 4 linhas preenchida com NA
mat.amostras = matrix(data = NA,
ncol = num.amostra,
nrow = n)
#Sorteando 1.000 amostras de tamanho 4 e armazenando-as na matriz mat.amostras
for(i in 1:num.amostra){
mat.amostras[,i] = sample(x = pop,
size = n,
replace = TRUE)
}
#Calcular a média para cada coluna de mat.amostras
media.amostral = apply(X = mat.amostras,
MARGIN = 2,
FUN = mean)
#Visualizar o histograma das médias amostrais e comparar com a densidade da distribuição Normal indicado pelo TLC
graf2 = ggplot(data = tibble(valores = media.amostral),
mapping = aes(x = valores)) +
geom_histogram(aes(y = after_stat(density)),
bins = 15) +
stat_function(fun = dnorm,
args = list(mean = med.pop,
sd = sqrt(var.pop/n)),
colour = "Red") +
labs(x = expression(bar(x)),
y = "Densidade",
title = "n = 4")
# -------------------- Executando para n = 20 ---------------------
#Vamos definir o tamanho da amostra que iremos trabalhar
n = 20
#Vamos definir o número de vezes que uma amostra de tamanho n será sorteada
num.amostra = 1000
#Definindo uma matriz com 1000 colunas e 20 linhas preenchida com NA
mat.amostras = matrix(data = NA,
ncol = num.amostra,
nrow = n)
#Sorteando 1.000 amostras de tamanho 20 e armazenando-as na matriz mat.amostras
for(i in 1:num.amostra){
mat.amostras[,i] = sample(x = pop,
size = n,
replace = TRUE)
}
#Calcular a média para cada coluna de mat.amostras
media.amostral = apply(X = mat.amostras,
MARGIN = 2,
FUN = mean)
#Visualizar o histograma das médias amostrais e comparar com a densidade da distribuição Normal indicado pelo TLC
graf3 = ggplot(data = tibble(valores = media.amostral),
mapping = aes(x = valores)) +
geom_histogram(aes(y = after_stat(density)),
bins = 15) +
stat_function(fun = dnorm,
args = list(mean = med.pop,
sd = sqrt(var.pop/n)),
colour = "Red") +
labs(x = expression(bar(x)),
y = "Densidade",
title = "n = 20")
# -------------------- Executando para n = 200 ---------------------
#Vamos definir o tamanho da amostra que iremos trabalhar
n = 200
#Vamos definir o número de vezes que uma amostra de tamanho n será sorteada
num.amostra = 1000
#Definindo uma matriz com 1000 colunas e 200 linhas preenchida com NA
mat.amostras = matrix(data = NA,
ncol = num.amostra,
nrow = n)
#Sorteando 1.000 amostras de tamanho 200 e armazenando-as na matriz mat.amostras
for(i in 1:num.amostra){
mat.amostras[,i] = sample(x = pop,
size = n,
replace = TRUE)
}
#Calcular a média para todas as colunas de mat.amostras
media.amostral = apply(X = mat.amostras,
MARGIN = 2,
FUN = mean)
#Visualizar o histograma das médias amostrais e comparar com a densidade da distribuição Normal indicado pelo TLC
graf4 = ggplot(data = tibble(valores = media.amostral),
mapping = aes(x = valores)) +
geom_histogram(aes(y = after_stat(density)),
bins = 15) +
stat_function(fun = dnorm,
args = list(mean = med.pop,
sd = sqrt(var.pop/n)),
colour = "Red") +
labs(x = expression(bar(x)),
y = "Densidade",
title = "n = 200")
#Ativando pacote
library(patchwork)
#Compondo uma figura
(graf1 | graf2)/ (graf3| graf4)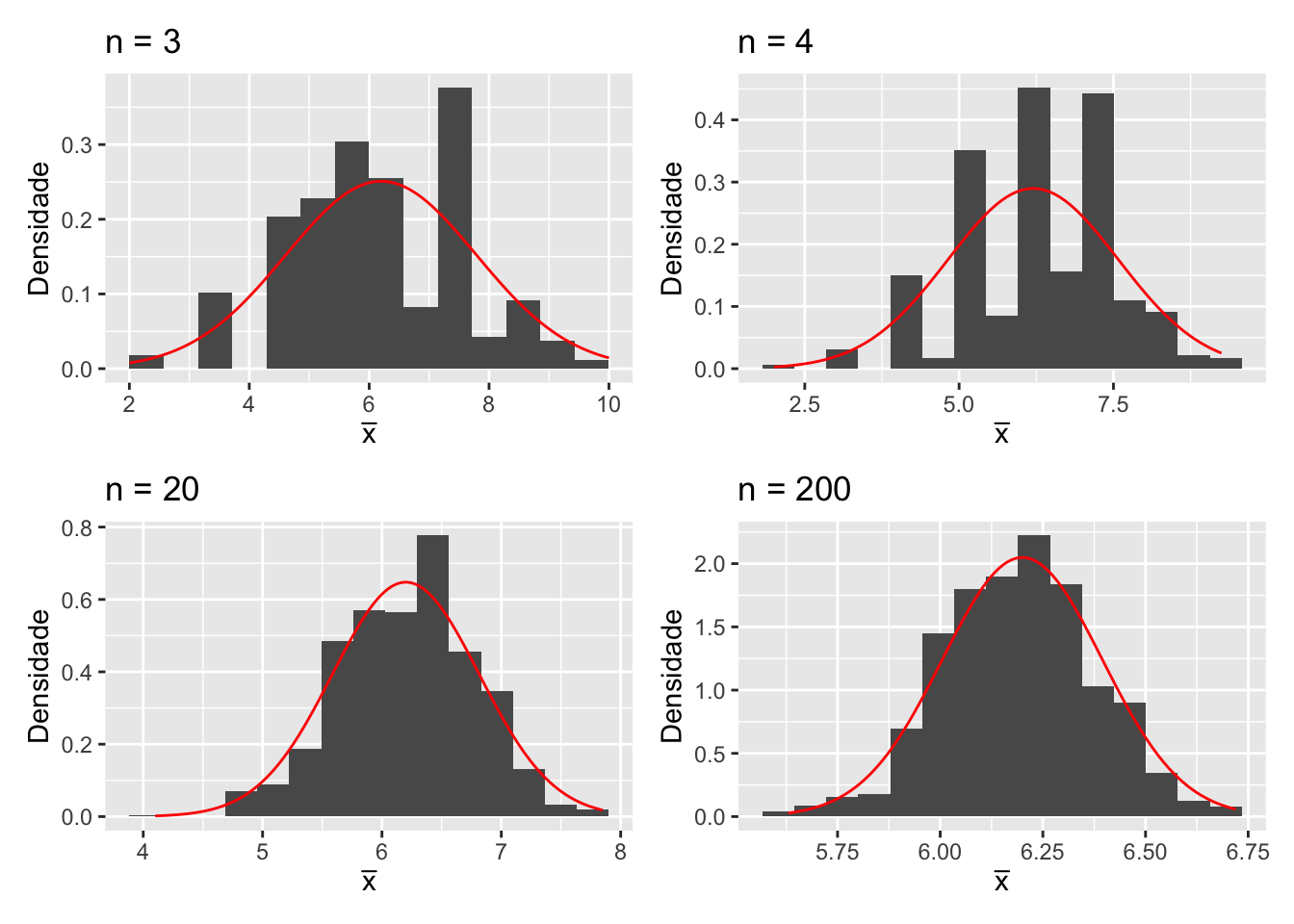
10.2 Distribuição Amostral da proporção
Agora, vamos analisar uma população em que a proporção de indivíduos com uma determinada característica é \(p\). Para isso, definiremos uma variável aleatória \(X\) da seguinte maneira:
\[X = \left \{ \begin{array}{cl} 1, & \mbox{se o indivíduo possui a característica de interesse} \\ 0, & \mbox{caso contrário} \\ \end{array} \right.\]
Deste modo, \(X \sim Bernoulli(p)\) com \[\mu = E(X) = p \mbox{ e } \sigma^2 = Var(X) = p(1-p).\]
Suponha que seja retirada uma amostra aleatória simples dessa população \((X_1,\ldots,X_n)\). Vamos denotar por \[Y_n = \displaystyle \sum_{i=1}^{n}X_i,\] o total de indivíduos portadores da característica na amostra. Sendo assim, \[Y_n \sim Binomial(n,p).\].
Vamos definir a proporção amostral de indivíduos portadores da característica na amostra como \[\hat{p}=\frac{Y_n}{n}.\]
Veja que \[\hat{p} = \bar{X}.\] Vimos que pelo TLC, quando \(n\) cresce, \[\bar{X} = \hat{p} \sim N\left(p, \frac{p(1-p)}{n} \right).\]
Vamos checar numericamente este resultado? Suponha que temos uma população em que \(p = 0,7\).
#Vamos definir o tamanho da amostra que iremos trabalhar
n = 700
#Vamos definir o número de vezes que uma amostra de tamanho n será sorteada
num.amostra = 10000
#Definindo uma matriz com 1000 colunas e 700 linhas preenchida com NA
mat.amostras = matrix(data = NA,
ncol = num.amostra,
nrow = n)
#Sorteando 1.000 amostras de tamanho 700 e armazenando-as na matriz mat.amostras
for(i in 1:num.amostra){
mat.amostras[,i] = sample(x = 0:1,
size = n,
prob = c(0.3,0.7),
replace = TRUE)
}
#Calcular a proporção (que neste caso é a média) para todas as colunas de mat.amostras
media.amostral = apply(X = mat.amostras,
MARGIN = 2,
FUN = mean)
#Visualizar o histograma das proporções amostrais e comparar com a densidade da distribuição Normal indicado pelo TLC
ggplot(data = tibble(valores = media.amostral),
mapping = aes(x = valores)) +
geom_histogram(aes(y = after_stat(density)),
bins = 15) +
stat_function(fun = dnorm,
args = list(mean = 0.7,
sd = sqrt((0.7*0.3)/n)),
colour = "Red") +
labs(x = expression(hat(p)),
y = "Densidade")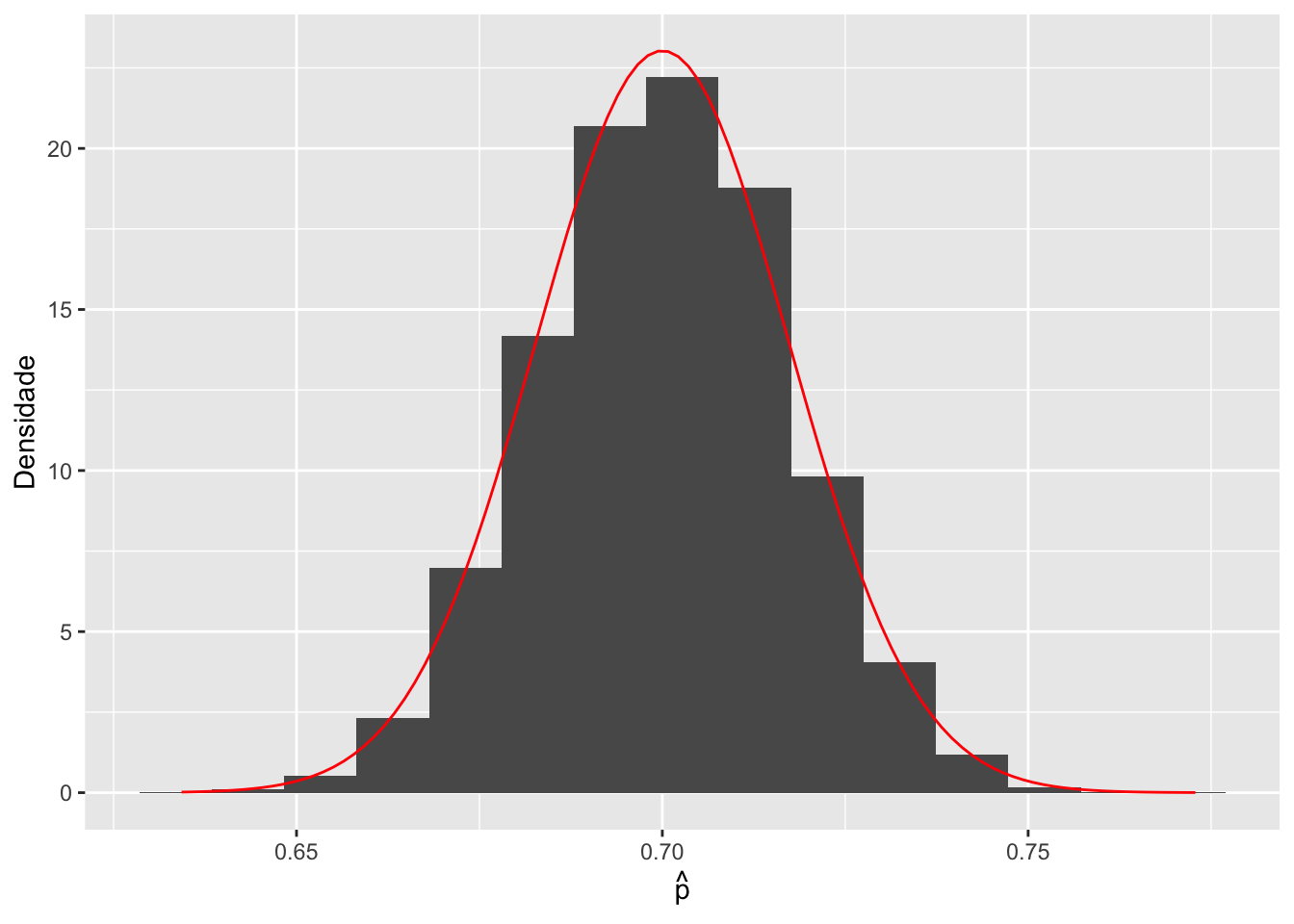
10.3 Outras Distribuições Amostrais
A seguir, examinaremos a distribuição amostral de uma estatística adicional, além da média e da proporção previamente abordada. Essas estatísticas são essenciais para efetuar inferências sobre parâmetros de interesse. Apresentaremos, de forma numérica, a distribuição amostral de uma estatística frequentemente empregada na elaboração de intervalos de confiança e na realização de testes de hipóteses.
Suponha que \(X \sim N(\mu,\sigma^2)\). Seja \(S^2 = \displaystyle\sum_{i=1}^n \dfrac{(X_i - \bar{X})^2}{n-1},\) o desvio padrão amostral. Existe um resultado que nos diz que a distribuição de \[ Q = \dfrac{(n-1)S^2}{\sigma^2} \sim \chi^2_{(n-1)}.\]
Como poderíamos validar esse resultado numericamente? Imagine que surja uma dúvida, ou seja, suponhamos que queiramos verificar se \[Q \sim \chi^2_{(2n)} \mbox{ ou } Q \sim \chi^2_{(n-1)}?\] Para ilustrar, considere \(n = 3\), \(\mu = 10\) e \(\sigma^2 = 25\). Seguiremos os passos a seguir.
#Definindo o objeto onde serão armazenads as amostras
#(cada coluna é uma amostra de tamanho 3)
amostra = matrix(data = NA,
ncol = 10000,
nrow = 3)
#Definindo o tamanho de cada amostra
n = 3
#Definindo o número de vezes que uma amostra de tamanho 3 será sorteada
num.amostra = 10000
#Sorteando 10.000 amostras de tamanho 3 de uma N(10,25) e armazenando cada amostra sorteada em uma coluna da matriz amostra
for(i in 1:num.amostra){
amostra[,i] = rnorm(n = n,
mean = 10,
sd = 5)
}
#Calculando a variância para cada coluna da matriz (para cada amostra sorteada)
variancia = apply(X = amostra,
MARGIN = 2,
FUN = var)
#Obtendo os valores de Q para cada amostra sorteada
valor_q = ((3 - 1)*variancia)/25
#Vamos plotar o histograma dos valores observados de Q e acrescentar sob o histograma
#a densidade teórica de uma distribuição qui-quadrado com n -1 = 2 graus de liberdade e a densidade teórica de uma distribuição qui-quadrado com 2n = 6 graus de liberdade
ggplot(data = tibble(valor_q),
mapping = aes(x = valor_q)) +
geom_histogram(mapping = aes(y = after_stat(density)),
binwidth = 1,
boundary = 0) +
stat_function(mapping = aes(colour = "qui-quadrado, gl = n-1"),
fun = dchisq,
args = list(df = 2)) +
stat_function(mapping = aes(colour = "qui-quadrado, gl = 2n"),
fun = dchisq,
args = list(df = 6)) +
labs(x = "q",
y = "densidade",
colour = "Distribuições")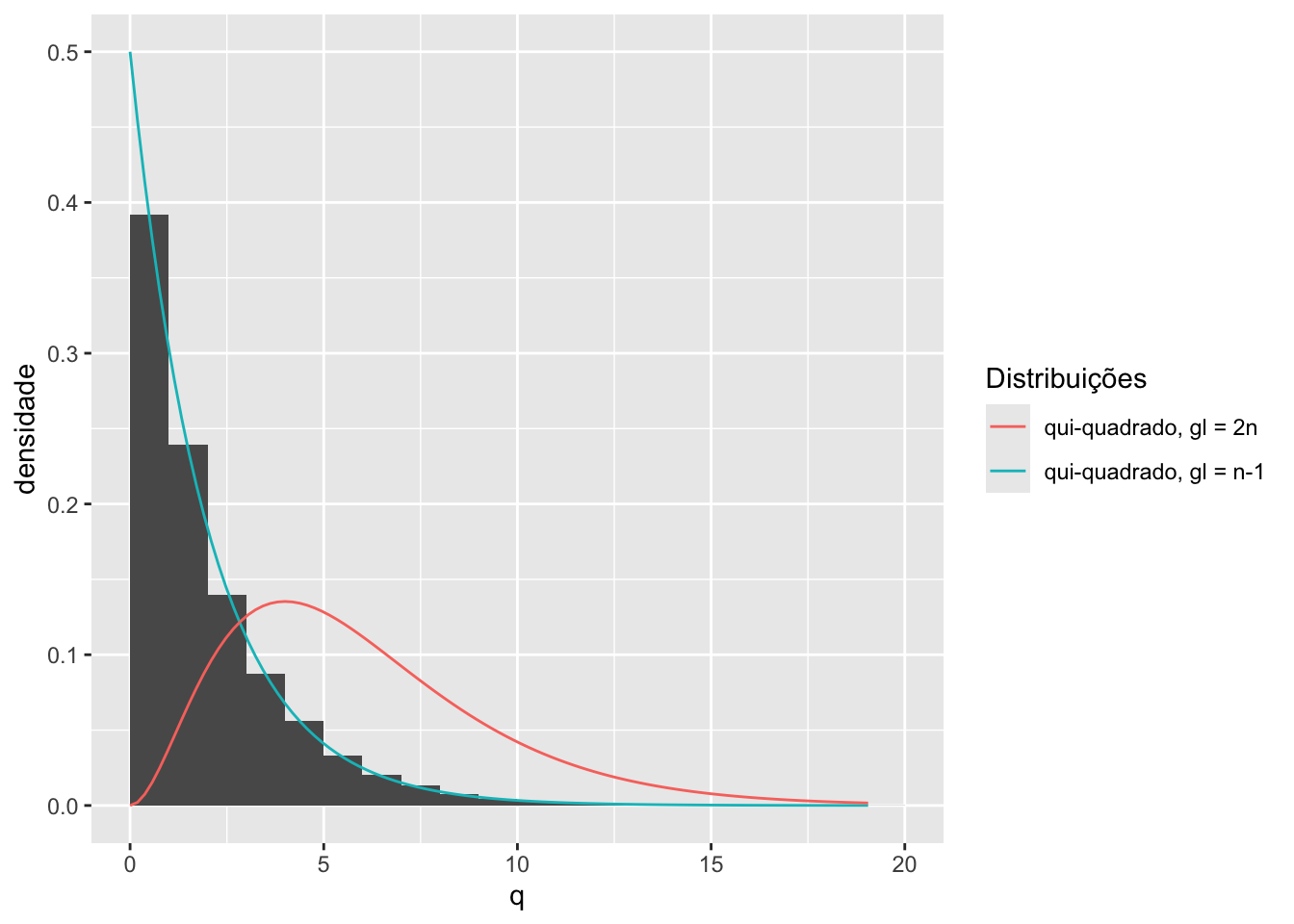
Pelo gráfico apresentado anteriormente, é evidente que o resultado \(Q \sim \chi^2_{(n-1)}\) parece plausível. O histograma das estimativas de \(Q\) se alinha bem com a função densidade de probabilidade de uma distribuição qui-quadrado com \(n-1\) graus de liberdade.
10.4 Procedimentos para checar resultados teóricos
Suponha que tenhamos \(X_1, \ldots, X_n\) como variáveis aleatórias. Consideremos \(g(X_1, \ldots, X_n)\) como uma transformação que envolve as \(n\) variáveis aleatórias, e seja o resultado \[g(X_1, \ldots, X_n) \sim f.\]Para verificar este resultado empiricamente, devemos:
- Amostrar \(N\) conjuntos de tamanho \(n\) das variáveis \(X\).
- Calcular \(g(X_1, \ldots, X_n)\) para cada uma das \(N\) amostras sorteadas.
- Comparar o histograma gerado a partir dos \(N\) valores de \(\hat{g}\) obtidos com a função densidade de probabilidade de \(f\).
Se o formato do histograma corresponder adequadamente à função densidade de probabilidade de \(f\), podemos concluir que, empiricamente, o resultado é plausível.
10.5 Desafio
Seja \(X \sim Exp(10)\). Considere que foram retiradas 1.000 amostras de tamanho 25 de \(X\). Obtenha a distribuição da mediana amostral e da variância amostral. Plote ambos os gráficos em uma mesma figura.
Seja \(X \sim N(10,25)\). Considere a estatística \[Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}.\]
Verifique empiricamente se \(Z \sim N(0,1)\), considerando a retirada de amostras de tamanho 30.
Seja \(X \sim N(10,\sigma^2)\). Considere a estatística \[T = \frac{\bar{X}-\mu}{S/\sqrt{n}} \sim t_{(n-1)}.\]
Verifique empiricamente se \(T \sim t_{(n-1)}\). Adote \(\mu = 50\) e \(n = 20\).