#Carregando pacote
library(readr)
#Importando os dados
base = read_table(file = "Maquinas.txt")22 Teste de hipóteses para comparação da proporção de duas populações
Vamos discutir o problema de se comparar duas proporções. Existem muitos cenários no qual desejamos comparar se as proporções de duas populações são iguais. Por exemplo, a proporção de homens favoráveis ao projeto de Lei Z é igual a proporção de mulheres favoráveis ao projeto de lei Z? Ou ainda, a proporção de clientes satisfeitos da operadora A é igual a proporção de clientes satisfeitos da operadora B?
Para respondermos os questionamentos acima precisamos fazer um teste de hipóteses comparando duas proporções.
Para exemplificarmos como realizar o teste no R, suponha agora que o dono de uma fábrica que produz o produto K, deseja saber se a proporção de itens defeituosos nas duas máquinas que estão operando na fábrica são iguais. Como proceder?
Antes de especificarmos hipóteses e testá-las podemos entender um pouco mais do problema realizando uma análise exploratória de dados.
#Visualizando os dados
base# A tibble: 45 × 3
Maquina Peso Defeito
<chr> <dbl> <dbl>
1 A 107. 0
2 B 144. 0
3 A 97.8 1
4 B 137. 0
5 A 101. 0
6 A 94.5 0
7 B 134. 1
8 A 99.9 0
9 A 94.4 0
10 B 141. 1
# ℹ 35 more rows#Tratando as variáveis
base$Maquina = factor(x = base$Maquina)
base$Defeito_cat = factor(x = base$Defeito,
labels = c("Não","Sim"))
#Ativando pacote
library(janitor)
#Tabela de contingência
base |>
tabyl(var1 = Defeito_cat,
var2 = Maquina) |>
adorn_percentages(denominator = "col") |> #calcula os % por coluna
adorn_pct_formatting(digits = 2) |> #apresenta os percentuais na escala de 0 a 100 com o símbolo %
adorn_ns() #inclui as frequências absolutas na tabela Defeito_cat A B
Não 72.00% (18) 70.00% (14)
Sim 28.00% (7) 30.00% (6)#Ativando pacote
library(ggplot2)
#Criando um gráfico apropriado
base |>
ggplot(mapping = aes(x = Maquina,
fill = Defeito_cat)) +
geom_bar(position = "fill") +
labs(x = "Máquina", y = "Porcentagem",fill = "Defeituoso") +
scale_y_continuous(labels = scales::percent_format()) +
theme_minimal()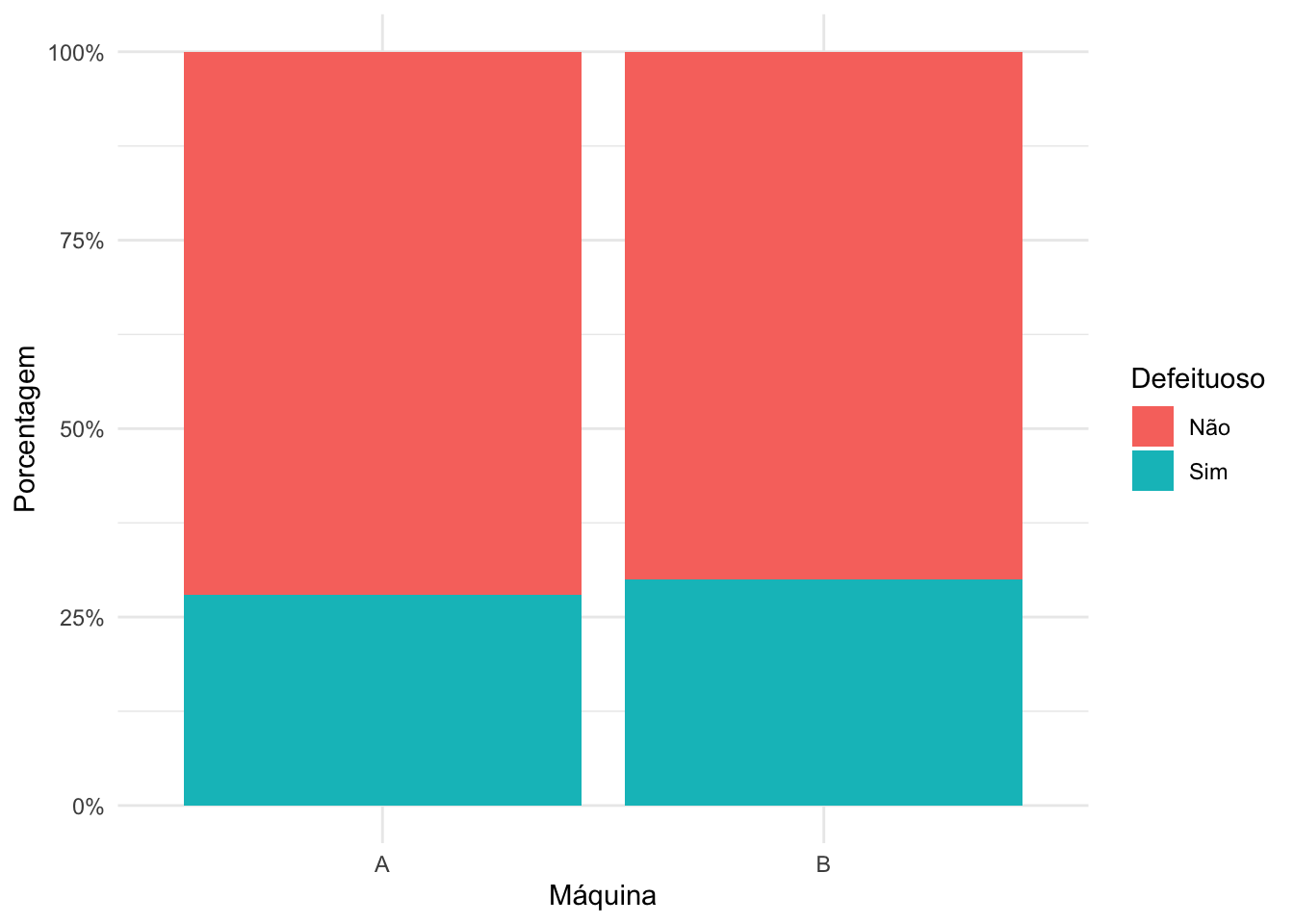
Se analisamos as tabelas e os gráficos produzidos, percebemos que as proporções de itens defeituosos nas duas máquinas parecem semelhantes, mas para fazermos tal afirmação precisamos realizar um teste de hipóteses.
Considere a proporção de itens defeituoso na máquina A (\(p_A\)) e a proporção de itens defeituoso na máquina B (\(p_B\)). Podemos especificar as seguintes hipóteses
Hipótese: \[H_0: p_A = p_B \qquad \times \qquad H_1: p_A \neq p_B,\] ou equivalentemente, \[H_0: p_A - p_B = 0 \qquad \times \qquad H_1: p_A - p_B \neq 0.\]
Para executarmos o teste acima, usaremos a função prop.test do pacote stats.
A seguir, vamos apresentar os principais argumentos da função prop.test:
- x - o vetor com o número de sucessos observados na amostra de cada população;
- n - o vetor com o tamanho da amostra retirado de cada população;
- alternative - argumento que define se o teste é bilateral ou unilateral a esquerda e a direita (default = bilateral - two.sided),
- correct - argumento que define se será aplicada a correção de continuidade na estatística de teste (default = TRUE).
#Ativando pacote
library(dplyr)
#Obtendo as quantidades necessárias para alimentar a função prop.test
resultados = base |>
group_by(Maquina) |>
summarise(N = n(),
favoraveis = sum(Defeito),
proporcao = favoraveis/N)
#Visualizando o objeto criado
resultados# A tibble: 2 × 4
Maquina N favoraveis proporcao
<fct> <int> <dbl> <dbl>
1 A 25 7 0.28
2 B 20 6 0.3 #Realizando o teste de igualdade de proporções
prop.test(x = c(resultados$favoraveis[1], resultados$favoraveis[2]),
n = c(resultados$N[1],resultados$N[2]),
alternative = "two.sided",
conf.level = 0.95,
correct = FALSE)
2-sample test for equality of proportions without continuity correction
data: c(resultados$favoraveis[1], resultados$favoraveis[2]) out of c(resultados$N[1], resultados$N[2])
X-squared = 0.021635, df = 1, p-value = 0.8831
alternative hypothesis: two.sided
95 percent confidence interval:
-0.2870446 0.2470446
sample estimates:
prop 1 prop 2
0.28 0.30 A saída do teste contém várias informações: o valor da estatística do teste \(X\)-squared, o número de graus de liberdade da estatística de teste \(df\) e o p-valor associado as hipóteses especificadas. Ele deixa explícito qual a hipótese alternativa “two.sided” que significa “as duas proporções são diferentes”. Fornece também um intervalo de confiança para a diferença entre as proporções e o valor da estimativa pontual da porporção em cada população.
Com base em um nível de significância de 5%, confirmamos aquele sentimento que adquirimos ao realizarmos a análise exploratória, pois p-valor = 0,8831 > 0,05 = \(\alpha\), logo não rejeitamos \(H_0\), indicando que as proporções de itens defeituosos produzidos pelas duas máquinas são iguais.
22.1 Desafio
Utilize o arquivo Dados socio.txt para responder as perguntas de 1 a 3 e utilizando o arquivo Maquinas.txt responda a questão 4.
Com base em um nível de significância de 5%, você diria que a proporçao de homens e mulhres com mais de 25 anos são iguais?
Com base em um nível de significância de 5%, você diria que a proporçao de homens com pesos superiores a 75 Kg é maior do que a de mulheres com peso superior a 75 kg?
O cliente é considerado como satisfeiro se a sua pontuação na satisfação é superior a 80 pontos. Com base em um nível de significância de 1%, você diria que a proproção de clientes satisfeitos do sexo masculino e feminino são iguais?
Verifique se a proporção de pacotes com mais de 100g produzidos por ambas as máquinas são iguais. Use um nível de significância de 5%.
Crie uma função que calcula o poder do teste para o teste de duas porporções unilateral a direita. Plote a função supondo \(\alpha = 0,05\), \(n_1 = 40\) e \(n_2 = 50\).