24  ANOVA

Agora vamos discutir o problema de se comparar a média de três ou mais populações.

Problema: um médico está avaliando três grupos de pacientes (controle, medicação e medicação + atividade). Ele gostaria de verificar se as médias de idade, glicemia e razão quadril/cintura difere entre os grupos.

Para respondermos o questionamento acima, precisamos realizar uma análise de variância - ANOVA. Vamos começar com a análise da variável idade. Porém, antes de especificarmos as hipóteses, sabemos que a ANOVA possui certos pressupostos que precisam ser checados, dentre eles, normalidade e homocedasticidade.

Abaixo podemos visualizar as variáveis que compõem a base de dados.

#Carregando pacote
library(readr)

#Importando os dados
base = read_csv2("base_tratamento.csv")
#Visualizando os dados
base
# A tibble: 60 × 4
   grupo    Idade glicemia   RQC
   <chr>    <dbl>    <dbl> <dbl>
 1 Controle    37    109.   1.36
 2 Controle    32    104.   1.23
 3 Controle    29    101.   1.26
 4 Controle    33    110.   1.32
 5 Controle    33     93    1.33
 6 Controle    35    103.   1.31
 7 Controle    33    104.   1.28
 8 Controle    36    107.   1.37
 9 Controle    40     97.1  1.35
10 Controle    36    111.   1.29
# ℹ 50 more rows

Vamos agora analisar a normalidade dos dados. Lembrando que é preciso analisar a normalidade em cada população. Como temos 3 (controle, medicação e medicação + atividade), faremos 3 qq-plots e 3 testes de normalidade.

#Ativando pacote
library(dplyr)

#Criando um tibble somente com as informações do grupo controle
baseA = base |> 
   filter(grupo == "Controle")

#Criando um tibble somente com as informações do grupo medicação
baseB = base |> 
   filter(grupo == "Medicação")

#Criando um tibble somente com as informações do grupo medicação + atividade
baseC = base |> 
   filter(grupo == "Medicação + Atividade")


#Carregando pacote
library(ggpubr)

#Criando um qq-plot com o ggpubr para a população 1
qq1 = ggqqplot(baseA$Idade)

#Criando um qq-plot com o ggpubr para a população 2
qq2 = ggqqplot(baseB$Idade)

#Criando um qq-plot com o ggpubr para a população 3
qq3 = ggqqplot(baseC$Idade)

#Carregando pacote
library(patchwork)

#Plotando os qqplots
(qq1 + qq2)/ qq3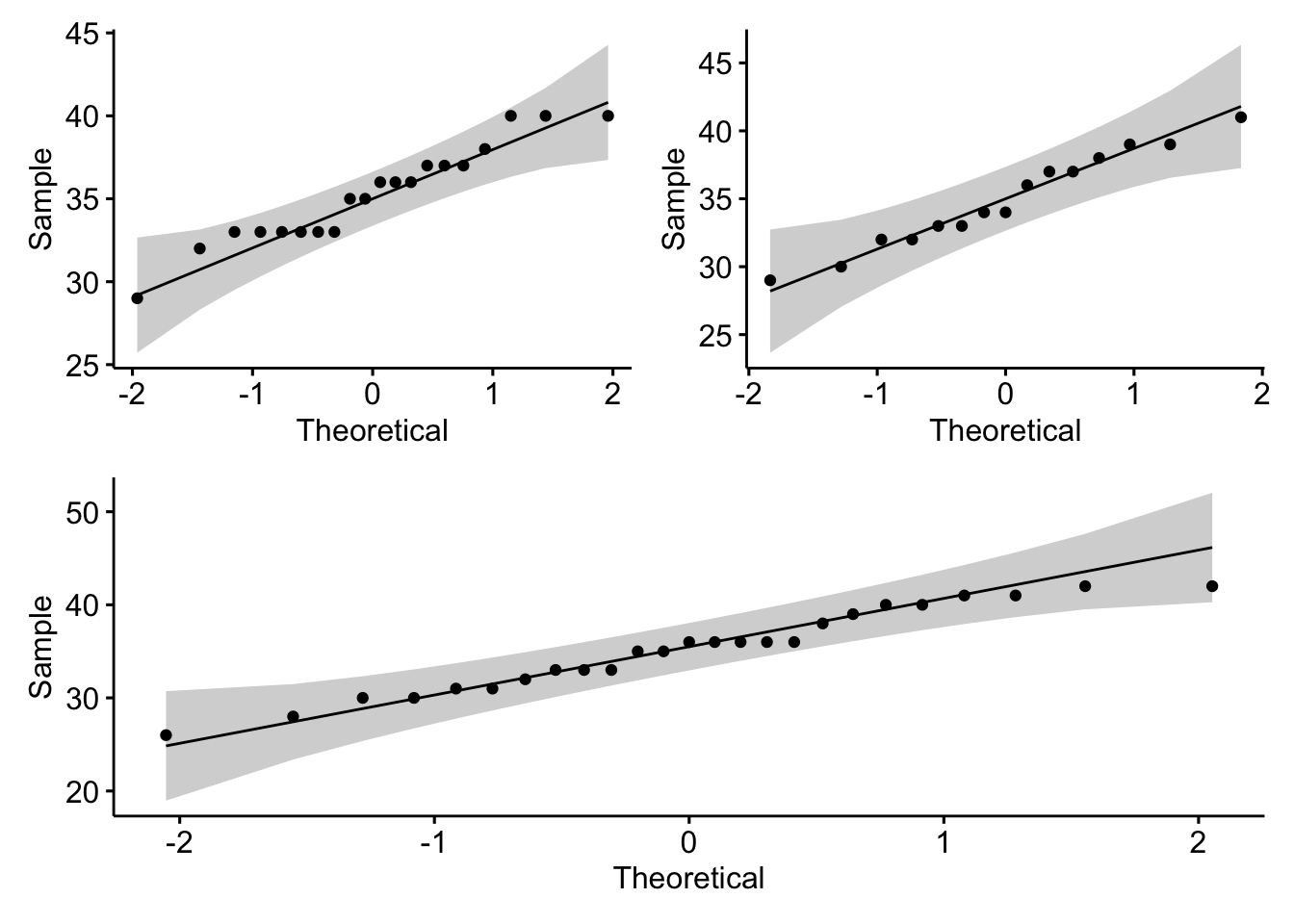

#Teste de normalidade para a população 1
shapiro.test(x = baseA$Idade)

    Shapiro-Wilk normality test

data:  baseA$Idade
W = 0.9397, p-value = 0.2367
#Teste de normalidade para a população 2
shapiro.test(x = baseB$Idade)

    Shapiro-Wilk normality test

data:  baseB$Idade
W = 0.96748, p-value = 0.8192
#Teste de normalidade para a população 3
shapiro.test(x = baseC$Idade)

    Shapiro-Wilk normality test

data:  baseC$Idade
W = 0.96181, p-value = 0.4518

Com base na análise acima, usando um nível de significância de 5%, concluímos que as amostras são provenientes de distribuições normais.

A seguir, vamos verificar a homocedasticidade, isto é,

Hipótese: \[H_0: \sigma^2_1 = \sigma^2_2 = \sigma^2_3 \qquad \times \qquad H_1: \mbox{Existe pelo menos uma variância diferente}.\]

Para executarmos o teste de comparação de variâncias, usaremos a função LeveneTest do pacote DescTools.

A seguir, vamos apresentar os principais argumentos da função LeveneTest:

  - y - o vetor com a amostra de todas as populações;

  - group - o vetor que indica a qual população a amostra pertence;

  - center - indica qual teste você deseja realizar (default = median - realiza o teste Brown-Forsythe-Test, se alimentarmos com o mean - realizamos o teste de Levene original).

#Carregando o pacote
library(DescTools)

#Avaliando as variâncias nas duas populações
base |> 
  group_by(grupo) |> 
  summarise(variâncias = var(Idade))
# A tibble: 3 × 2
  grupo                 variâncias
  <chr>                      <dbl>
1 Controle                    8.75
2 Medicação                  12.5 
3 Medicação + Atividade      20.1 
#Realizando o teste de comparação das variâncias
LeveneTest(y = base$Idade, 
           group = base$grupo, 
           center = "mean")
Warning in LeveneTest.default(y = base$Idade, group = base$grupo, center =
"mean"): base$grupo coerced to factor.
Levene's Test for Homogeneity of Variance (center = "mean")
      Df F value Pr(>F)
group  2  1.9839 0.1469
      57

Avaliando as estimativas pontuais, aparentemente o grupo Atividade + Medicação possui uma variância para a idade maior, mas este resultado não se confirma com o teste de Levene. Com base em um nível de significância de 5%, não rejeitamos a hipótese de igualdade das variâncias.

Após checarmos normalidade e homocedasticidade, podemos comparar as médias de idade. Notem que, se alguma população não possuísse normalidade e/ou não fosse detectado homocedasticidade não poderíamos prosseguir com a análise.

No problema levantado queremos testar as seguintes hipóteses

Hipótese: \[H_0: \mu_1 = \mu_2 = \mu_3 \qquad \times \qquad H_1: \mbox{Existe pelo menos uma média diferente}.\]

Vamos realiazar uma análise exploratória dos dados, antes de realizarmos o teste de comparação de médias.

#Comparando os grupos descritivamente
base |> 
  group_by(grupo) |> 
  summarise(medias = mean(Idade))
# A tibble: 3 × 2
  grupo                 medias
  <chr>                  <dbl>
1 Controle                35.3
2 Medicação               34.9
3 Medicação + Atividade   35.2
#Ativando pacote
library(ggplot2)

#Comparando os grupos graficamente
ggplot(data = base, aes(x = grupo, y = Idade)) +
  geom_boxplot() +
  theme_classic2() +
  labs(x = "Grupo",
       y = "Idade")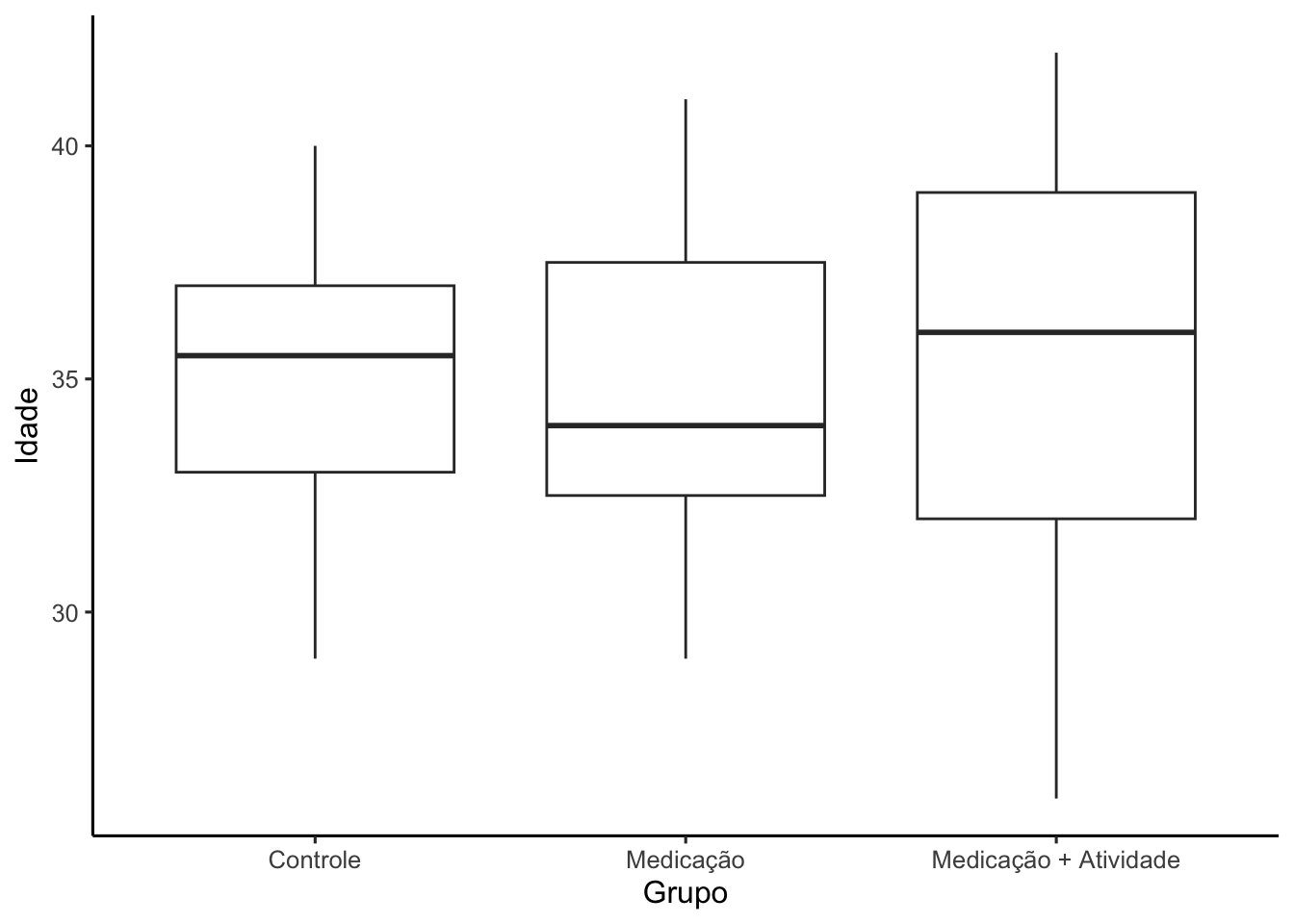

Para executarmos o teste de comparação das médias, usaremos a função aov.

A seguir, vamos apresentar os principais argumentos da função aov:

  - formula - o vetor com a amostra;

  - mu - o valor do parâmetro que definem as hipóteses (default = 0);

  - alternative - argumento que define se o teste é bilateral ou unilateral a esquerda e a direita (default = bilateral - two.sided).

#Realizando o teste de comparação das médias
comp1 = aov(formula = Idade ~ grupo, 
            data = base)

#Visualizando o resultado
summary(comp1)
            Df Sum Sq Mean Sq F value Pr(>F)
grupo        2    1.2    0.60   0.042  0.959
Residuals   57  823.1   14.44

Note que, as estimativas pontuais parecem muito semelhantes. Com base em um nível de significância de 5%, não rejeitamos \(H_0\), isto é, não encontramos evidências para acreditar que as idades médias das três populações sejam diferentes.

E se o nosso desejo for comparar a glicemia dos três grupos? Vamos usar um nível de significância de 1%.

#Criando um qq-plot com o ggpubr para a população 1
qq_1 = ggqqplot(baseA$glicemia)

#Criando um qq-plot com o ggpubr para a população 2
qq_2 = ggqqplot(baseB$glicemia)

#Criando um qq-plot com o ggpubr para a população 3
qq_3 = ggqqplot(baseC$glicemia)


#Plotando os qqplots
(qq_1 + qq_2) / qq_3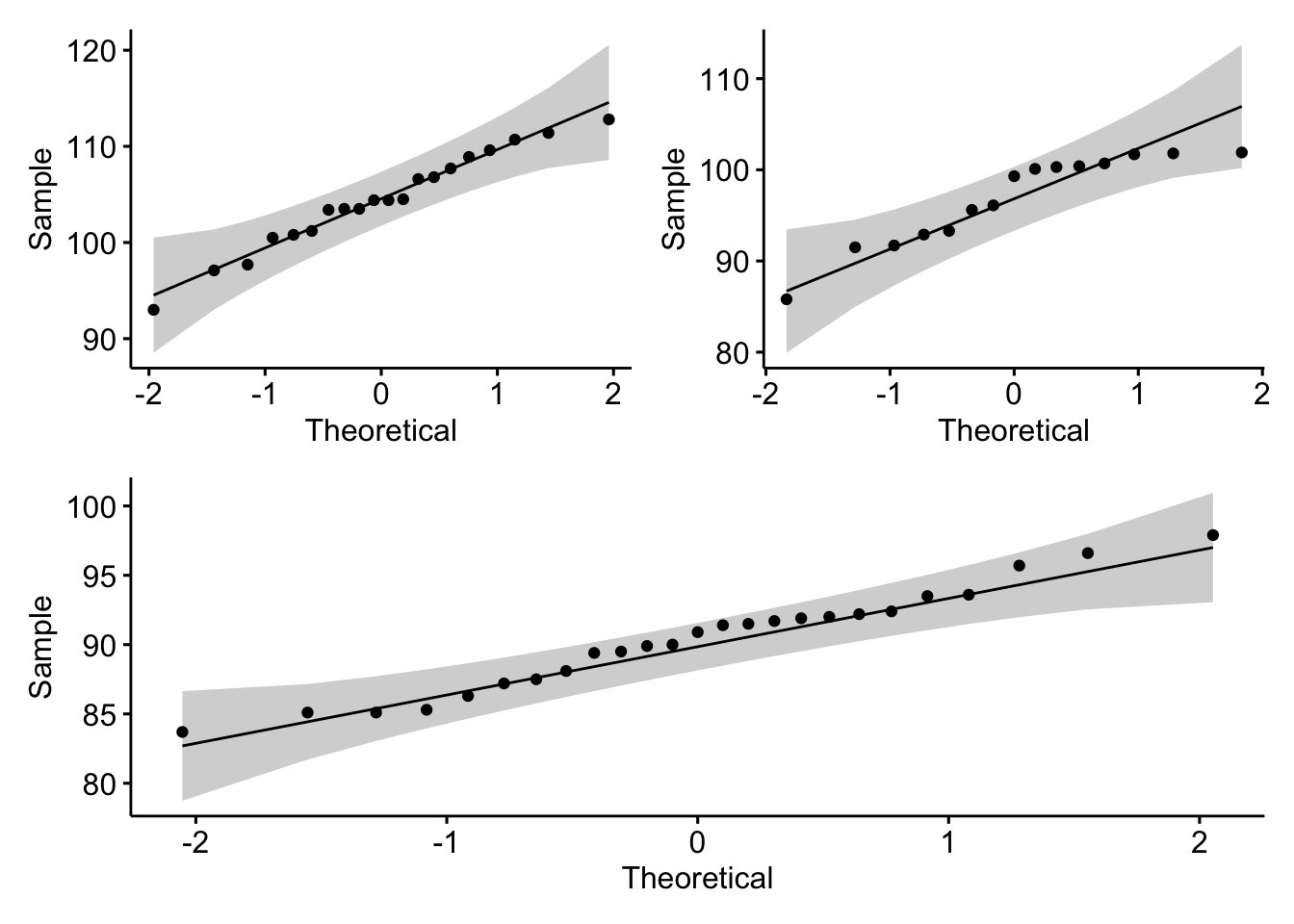

#Teste de normalidade para a população 1
shapiro.test(x = baseA$glicemia)

    Shapiro-Wilk normality test

data:  baseA$glicemia
W = 0.97659, p-value = 0.8829
#Teste de normalidade para a população 2
shapiro.test(x = baseB$glicemia)

    Shapiro-Wilk normality test

data:  baseB$glicemia
W = 0.87838, p-value = 0.04488
#Teste de normalidade para a população 3
shapiro.test(x = baseC$glicemia)

    Shapiro-Wilk normality test

data:  baseC$glicemia
W = 0.97381, p-value = 0.742
#Avaliando as variâncias nas duas populações
base |> 
  group_by(grupo) |> 
  summarise(variâncias = var(glicemia),
            medias = mean(glicemia))
# A tibble: 3 × 3
  grupo                 variâncias medias
  <chr>                      <dbl>  <dbl>
1 Controle                    26.2  104. 
2 Medicação                   24.1   96.9
3 Medicação + Atividade       13.7   90.3
#Comparando os grupos graficamente
ggplot(data = base, aes(x = grupo, y = glicemia)) +
  geom_boxplot() +
  labs(x = "Grupo",
       y = "Glicemia") +
  theme_minimal()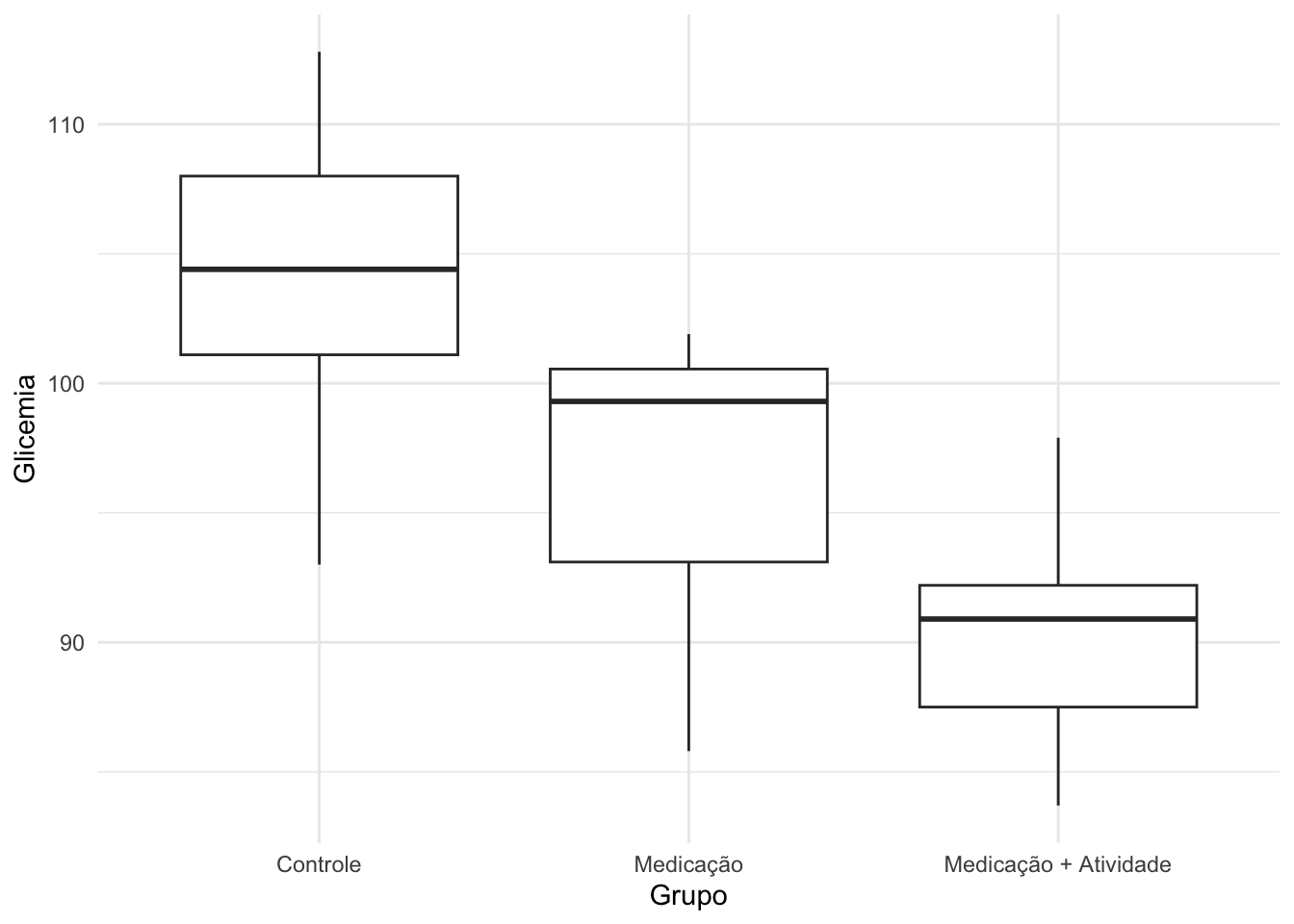

#Realizando o teste de comparação das variâncias
LeveneTest(y = base$glicemia, 
           group = base$grupo, 
           center = "mean")
Warning in LeveneTest.default(y = base$glicemia, group = base$grupo, center =
"mean"): base$grupo coerced to factor.
Levene's Test for Homogeneity of Variance (center = "mean")
      Df F value Pr(>F)
group  2  1.2919 0.2827
      57               
#Realizando o teste de comparação das médias
comp2 = aov(formula = glicemia ~ grupo, 
            data = base)

#Visualizando o resultado
summary(comp2)
            Df Sum Sq Mean Sq F value   Pr(>F)    
grupo        2   2206  1103.2   54.07 6.82e-14 ***
Residuals   57   1163    20.4                     
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Comentários de cada passo da análise:

*Com base em um nível de significância de 1%, rejeitamos \(H_0\), indicando que possuímos evidências suficiente para acreditar que existe pelo menos uma glicemia média diferente das demais.

O resultado de diferênça entre as médias apontado pela ANOVA não nos permite dizer entre quais grupos as médias são diferentes, por isso precisamos realizar um teste de comparações múltiplas.

Existem diversos testes de comparações múltiplas disponíveis na literatura, aqui vamos investigar alguns destes testes.

#Realizando o teste de Tuckey
TukeyHSD(x = comp2)
  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = glicemia ~ grupo, data = base)

$grupo
                                      diff       lwr        upr     p adj
Medicação-Controle               -7.551667 -11.26437  -3.838963 0.0000250
Medicação + Atividade-Controle  -14.089000 -17.34990 -10.828095 0.0000000
Medicação + Atividade-Medicação  -6.537333 -10.08736  -2.987310 0.0001262
#Realizando o teste de Duncan
PostHocTest(x = comp2, 
            method = "duncan")

  Posthoc multiple comparisons of means : Duncan's new multiple range test 
    95% family-wise confidence level

$grupo
                                      diff     lwr.ci     upr.ci    pval    
Medicação-Controle               -7.551667 -10.641138  -4.462195 8.5e-06 ***
Medicação + Atividade-Controle  -14.089000 -16.943402 -11.234598 5.6e-12 ***
Medicação + Atividade-Medicação  -6.537333  -9.491433  -3.583233 4.3e-05 ***

---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Tanto o teste de Tukey quanto o teste de Duncan indicam que as médias dos três grupos são diferentes.

24.1 Desafio

Resolva os exercícios de 2 a 4 usando o arquivo Escalas psicometricas.tx. Nas três escalas, quanto maior a pontuação, pior o desempenho do paciente.

  1. Usando a base discutida ao longo da aula, verifique se existe diferença na média da razão cintura quadril entre os três grupos. utilize um nível de significância de 5%.

  2. Usando um nível de significância de 5%, existe diferença na pontuação do MEEM entre os três grupos?

  3. Ao nível de significância de 5%, é correto afirmar que o desempenho de pacientes com Alzheimer e Demência são iguais e que eles diferem do grupo controle para a pontuação no CAMCOG?

  4. Usando um nível de significância de 1%, existe diferença na pontuação do teste do relógio entre os três grupos?