#função de verossimilhança
f.vero = function(x,lambda){
n = length(x)
aux = lambda^n*exp(-lambda*sum(x))
return(aux)
}
#Aplicando a funÇão na amostra x = (2,4,1,3,4) e lambda = 5
f.vero(c(2,4,1,3,4), lambda = 5)[1] 1.242328e-2712 Estimadores de Máxima Verossimilhança
Este capítulo traz uma discussão sobre como obter estimativas de máxima verossimilhança, isto é, como obter estimativas para os estimadores de máxima verossimilhança.
12.1 Príncipio da máxima verossimilhança
O princípio da verossimilhança sugere que deve ser escolhido o valor do parâmetro populacional desconhecido que maximiza a probabilidade de obter a amostra que de fato observada. Deste modo, é sugerido que escolhamos o valor que torna essa amostra a mais provável. Seguir esse princípio leva a um método de estimação que resulta nos estimadores de máxima verossimilhança, os quais geralmente apresentam propriedades altamente desejáveis.
12.2 Função de verossimilhança
Seja uma variável aleatória \(X\) com função densidade de probabilidade \(f(x|\theta)\). Seja \(X_1, \ldots, X_n\) uma amostra aleatória simples de \(X\). A função de verossimilhança de \(\theta\) será definida por
\[L(\theta|x_1,\ldots,x_n) = f(x_1|\theta) \times \ldots \times f(x_n|\theta),\] que deve ser encarada como uma função de \(\theta\). Chamaremos de função de log-verossimilhança
\[l(\theta|x_1,\ldots,x_n) = log(L(\theta|x_1,\ldots,x_n)).\]
Suponha que \(X \sim Exp(\lambda)\). A função de verossimilhança de \(\lambda\) será dada por
\[\begin{eqnarray} L(\lambda|x_1,\ldots,x_n) & = & f(x_1|\lambda) \times \ldots \times f(x_n|\lambda) \\ & = & \lambda e^{-\lambda x_1} \times \ldots \times \lambda e^{-\lambda x_n} \\ & = & \lambda^n e^{- \lambda \sum_{i=1}^{n} x_i}, \end{eqnarray}\]e a função de log-verossimilhança será dada por
\[\begin{eqnarray} l(\lambda|x_1,\ldots,x_n) & = & log(L(\lambda|x_1,\ldots,x_n)) \\ & = & log\left(\lambda^n e^{- \lambda \sum_{i=1}^{n} x_i}\right), \\ & = & n log(\lambda) - \lambda \sum_{i=1}^{n}x_i. \end{eqnarray}\]O estimador de máxima verossimilhança é aquele que maximiza \(L(\lambda|x_1,\ldots,x_n)\). Vamos incialemente plotar a função de verossimilhança de interesse. Para tal, vamos construir uma função no R que calcula o valor da verossimilhança.
Agora vamos plotar a função \(L(\lambda|x_1,\ldots,x_n)\) assumindo que foram observados os valores x = (0.1, 0.2, 0.1, 0.3, 0.4, 0.1, 0.2, 0.2, 0.2).
#Pacote
library(ggplot2)
library(tibble)
#valores de x observados
val_x = c(0.1,0.2,0.1,0.3,0.4,0.1,0.2,0.2,0.2)
#plotando L
L = ggplot(data = tibble(x = c(0,15)),
mapping = aes(x = x)) +
stat_function(fun = f.vero,
args = list(x = val_x)) +
labs(y = expression(L(lambda)),
x = expression(lambda)) +
scale_x_continuous(breaks = 0:15)
L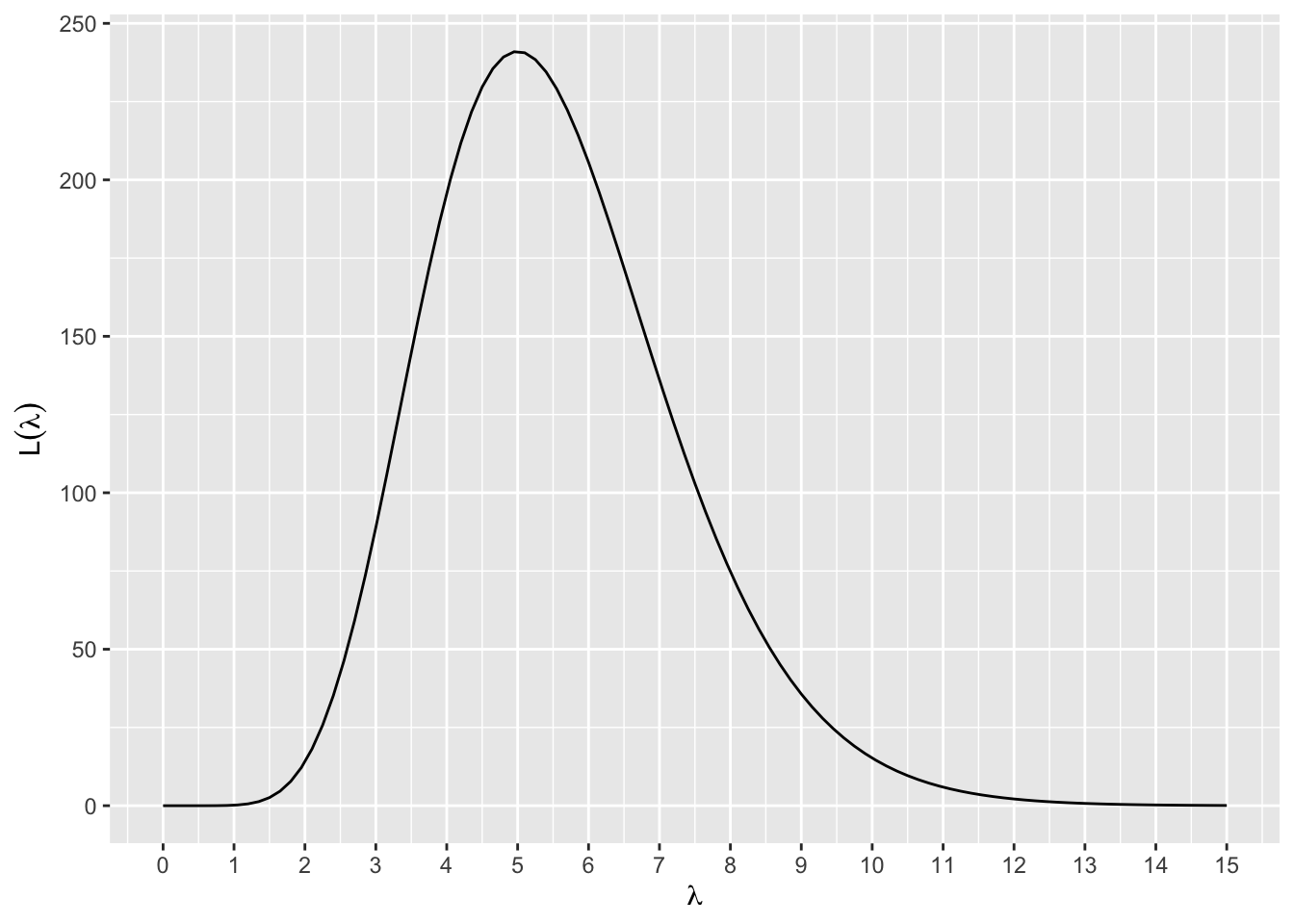
O gráfico acima apresenta o comportamento da função de verossimilhança para \(0< \lambda < 15\). Como definir o intervalo para plotar a função de verossimilhança? Isso vai depender o parâmetro que estamos estimando. Perceba que \(\lambda > 0\), logo não faria sentido olharmos o compartamento de \(L\) para valores negativos.
A seguir vamos utilizar a função optimeze para encontrar o máximo da função de verossimilhança. Os principais argumentos da função são:
f- a função que você deseja maximizar;interval- o intervalo no qual você irá buscar o máximo da função;maximum- um argumento lógico indicando se a função será maximizada ou minimizada (default = FALSE).
Caso a função possua outros argumnentos além do parâmetro de interesse, esses argumentos precisam ser informados, como é o caso de x que na nossa função f.vero representa o vetor com a amostra.
#Obtendo o máximo da função de verossimilhança
estMV = optimize(f = f.vero,
interval = c(0,15),
maximum = TRUE,
x = val_x)
estMV$maximum
[1] 4.999997
$objective
[1] 241.0348A função optimize retorna dois valores: maximum e objective. O maximum representa o valor de \(\lambda\) que maximiza a função \(L(\lambda|x_1,\ldots,x_n)\), isto é \[ \mbox{maximum } = \hat{\lambda}_{MV}. \]
Já o objective é o valor da função de verossimilhança avaliada no maximum, isto é, \[ \mbox{objective } = L(\hat{\lambda}_{MV}). \] Vamos plotar uma reta em \(\hat{\lambda}_{MV}\).
#incluindo uma reta vertical na estimativa de máxima verossimilhança
graf1 = L +
geom_vline(xintercept = estMV$maximum,
color = "red")
graf1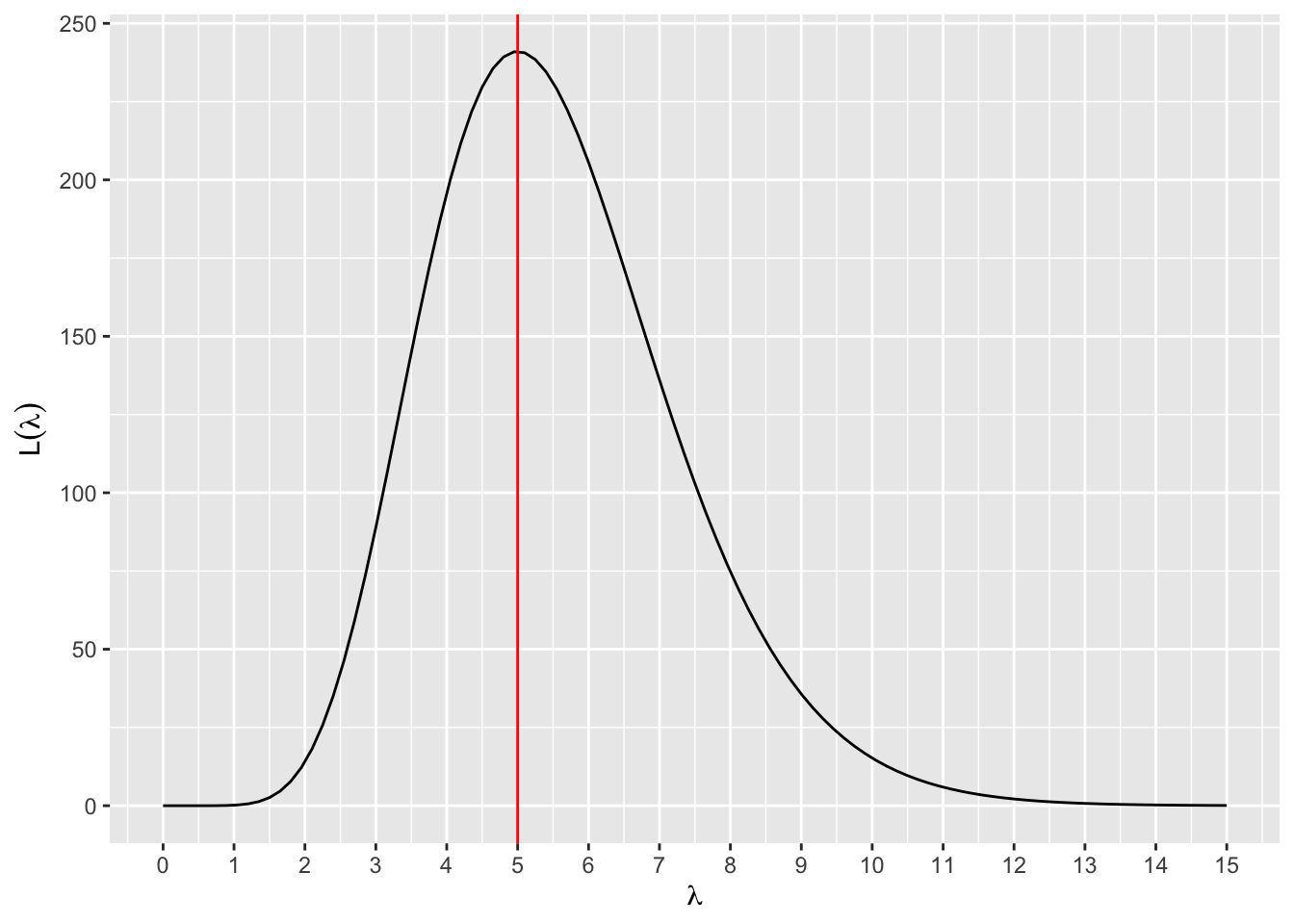
Se em vez de maximizar a função de verossimilhança, optássemos por maximizar a função de log-verossimilhança, alcançaríamos o mesmo resultado? Vamos seguir os seguintes passos:
- Criar uma função que calcula a log-verossimilhança de uma Exponencial(\(\lambda\)).
- Obter \(\lambda\) que maximiza \(l(\lambda,x_1,\ldots,x_n)\).
- Plotar a função de log-verossimilhança e uma reta vertical no eixo \(x\) que apresenta a estimativa de \(\lambda\).
#função de log-verossimilhança
f.log.vero = function(x,lambda){
n = length(x)
aux = n*log(lambda)-lambda*sum(x)
return(aux)
}
#Obtendo o máximo da função de log-verossimilhança
estMV_log = optimize(f = f.log.vero,
interval = c(0,15),
maximum = TRUE,
x = val_x)
#Plotando a função de log-verossimilhança e o seu máximo
graf2 = ggplot(data = tibble(x = c(0,15)),
mapping = aes(x = x)) +
stat_function(fun = f.log.vero,
args = list(x = val_x)) +
labs(y = expression(L(lambda)),
x = expression(lambda)) +
scale_x_continuous(breaks = 0:15) +
geom_vline(xintercept = estMV_log$maximum,
color = "blue")
graf2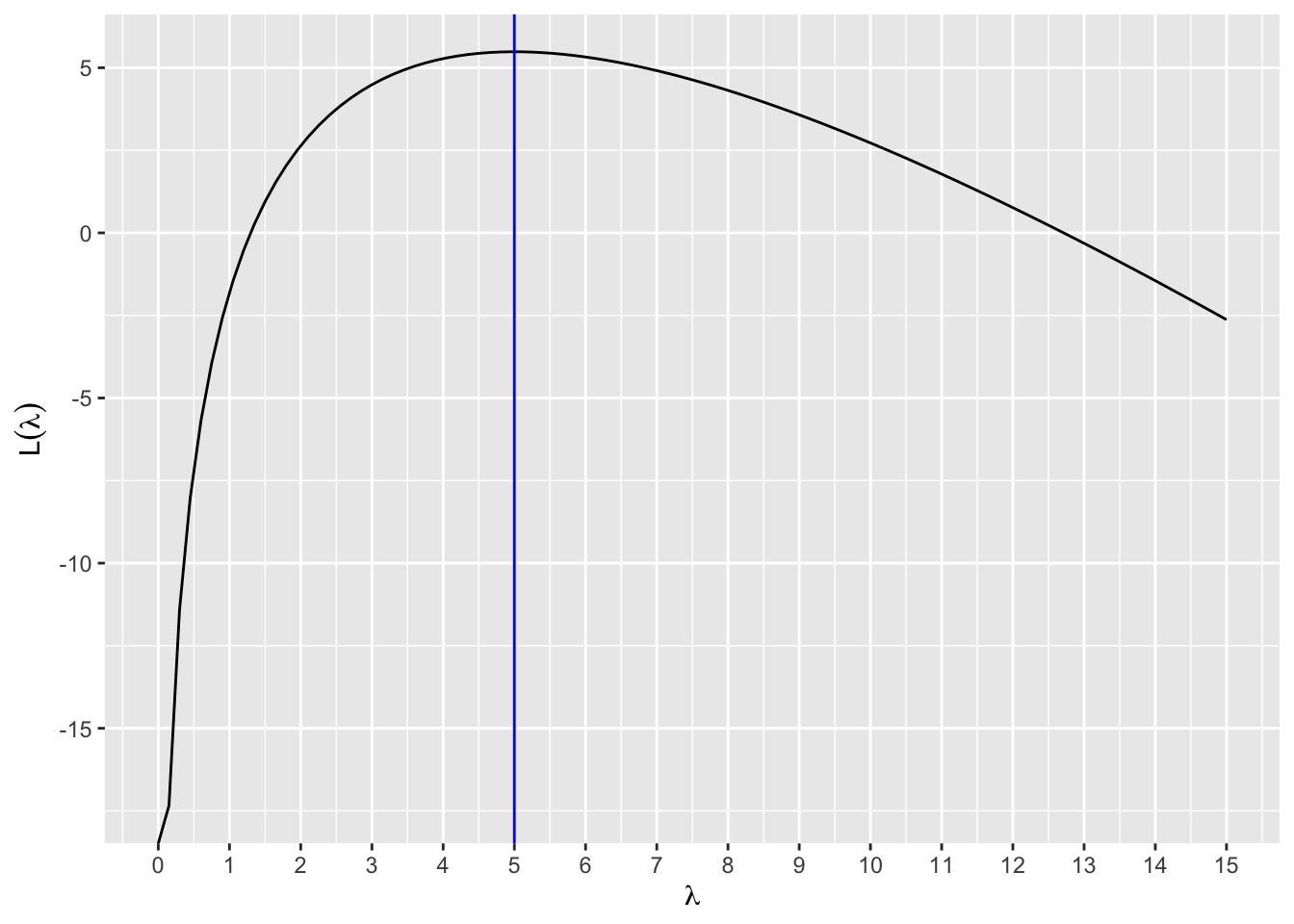
O valor que maximiza a função de verossimilhança é o mesmo que maximiza a função de log-verossimilhança.
12.3 Desafio
Apresente uma estimativa para o estimador de máxima verossimilhança de \(\beta\) se \(X \sim Gama(2,\beta)\). Suponha que foram observada uma amostra de 10 valores: 0.26231658, 0.14643441, 0.14282051, 0.09734330, 0.55265158, 0.07529625, 0.09437174, 0.20535829, 0.31079657 e 0.28721392.
Plote a função de log-verossimilhança para \(\lambda\) se \(X \sim Poisson(\lambda)\). Plote no gráfico da função de log-verossimilhança a estimativa de máxima verossimilhança de \(\lambda\) para a amostra 3, 0, 2, 3, 0, 2, 3, 1, 0, 2, 2, 3, 2, 2 e 0.
12.4 Propriedades dos estimadores
Ao obter estimadores para os parâmetros, é desejável que estes apresentem certas propriedades, como viés e consistência. Suponhamos uma população composta pelos valores 2, 6, 6, 7 e 10. Qual o valor da média populacional (\(\mu\)) neste caso? Vemos que \[\mu = \dfrac{2 + 6 + 6 + 7 + 10}{5} = 6,2.\] Suponha agora, que estamos usando o estimador \[\bar{X} = \sum_{i=1}^{n}\dfrac{X_1 + X_2 + \ldots + X_n}{n},\]para fazermos inferência sobre \(\mu\).
12.5 Estimadores não-viesados
Um estimador \(T\) é não-viesado para \(\theta\) se
\[ E(T) = \theta. \]
Como podemos verificar numericamente esse resultado para a população de interesse levantada anteriormente? Se sorteássemos todas as amostras aleatórias simples de tamanho \(n=3\) dessa população e calculássemos a média amostral de cada uma, e depois a média dessas médias amostrais, qual seria esse valor esperado?
#Definindo a nossa população
pop = c(2, 6, 6, 7, 10)
#Vamos definir o número de amostras de tamanho n que serão sorteadas
num.amostra = 10000
#Definindo o tamanho de cada amostra sorteada
n = 3
#Definindo uma matriz com 10000 colunas e 3 linhas preenchida com NA
mat.amostras = matrix(data = NA,
ncol = num.amostra,
nrow = n)
#Sorteando 1.000 amostras de tamanho 2 e armazenando cada amostra sorteada em uma coluna da matriz mat.amostras
for(i in 1:num.amostra){
mat.amostras[,i] = sample(x = pop,
size = n,
replace = TRUE)
}
#Calcular a média para cada coluna da matriz
media.amostral = apply(X = mat.amostras,
MARGIN = 2,
FUN = mean)
#Calculando a média das médias amostrais
medXbarra = mean(media.amostral)
medXbarra[1] 6.189067Podemos perceber que a média das médias amostrais é bem próxima ao valor da média populacional \(\mu\).
12.6 Estimadores consistentes
É possível checarmos numericamente se \(\bar{X}\) é um estimador consistente para \(\mu\)? Como responder ao questionamento levantado?
Relembrando que uma sequência \(T_n\) de estimadores de \(\theta\) é consistente se \[ lim_{n \rightarrow \infty }E(T_n) = \theta \quad \mbox{e} \quad lim_{n \rightarrow \infty }Var(T_n) = 0.\]
#Definindo a nossa população
pop = c(1,3,5,5,7)
#Vamos definir o número de amostras de tamanho n que serão sorteadas
num.amostra = 1000
#Definindo os diferentes tamanhos de amostras
n = c(2,5,10,50,100,500,10000)
#Definindo o objeto que guadará as variâncias do estimador X.barra
varEst = NULL
#Vamos investigar a variância de X.barra em 7 cenários (valores distintos de n)
for(i in 1:length(n)){
#Vamos criar o objeto que armazenará as amostras de tamanho n sorteadas
mat.amostras = matrix(NA,
ncol = num.amostra,
nrow = n[i])
#Vamos sortear as 1000 amostras de tamanho n
for(j in 1:num.amostra){
mat.amostras[,j] = sample(x = c(1,3,5,5,7),
size = n[i],
replace = TRUE)
}
#Vamos calcular o nosso estimador para cada amostra obtida
media.amostral = apply(X = mat.amostras,
MARGIN = 2,
FUN = mean)
#Calcular a variância das estimativas das médias amostrais obtidas
varEst[i] = var(media.amostral) #Essa medida é uma estimativa para Var(X.barra)
}
#Ativando pacote
library(tibble)
#Armazenando a variância do estimador X.barra e n
resultados = tibble(n = n, variancia = varEst)
#Visualizando os resultados obtidos
resultados# A tibble: 7 × 2
n variancia
<dbl> <dbl>
1 2 2.04
2 5 0.822
3 10 0.428
4 50 0.0789
5 100 0.0414
6 500 0.00831
7 10000 0.000433#Visualizando graficamente
resultados |>
ggplot(mapping = aes(x = factor(n),
y = variancia)) +
geom_bar(stat = "identity") +
labs(x = "n",
y = expression(Var(bar(X))))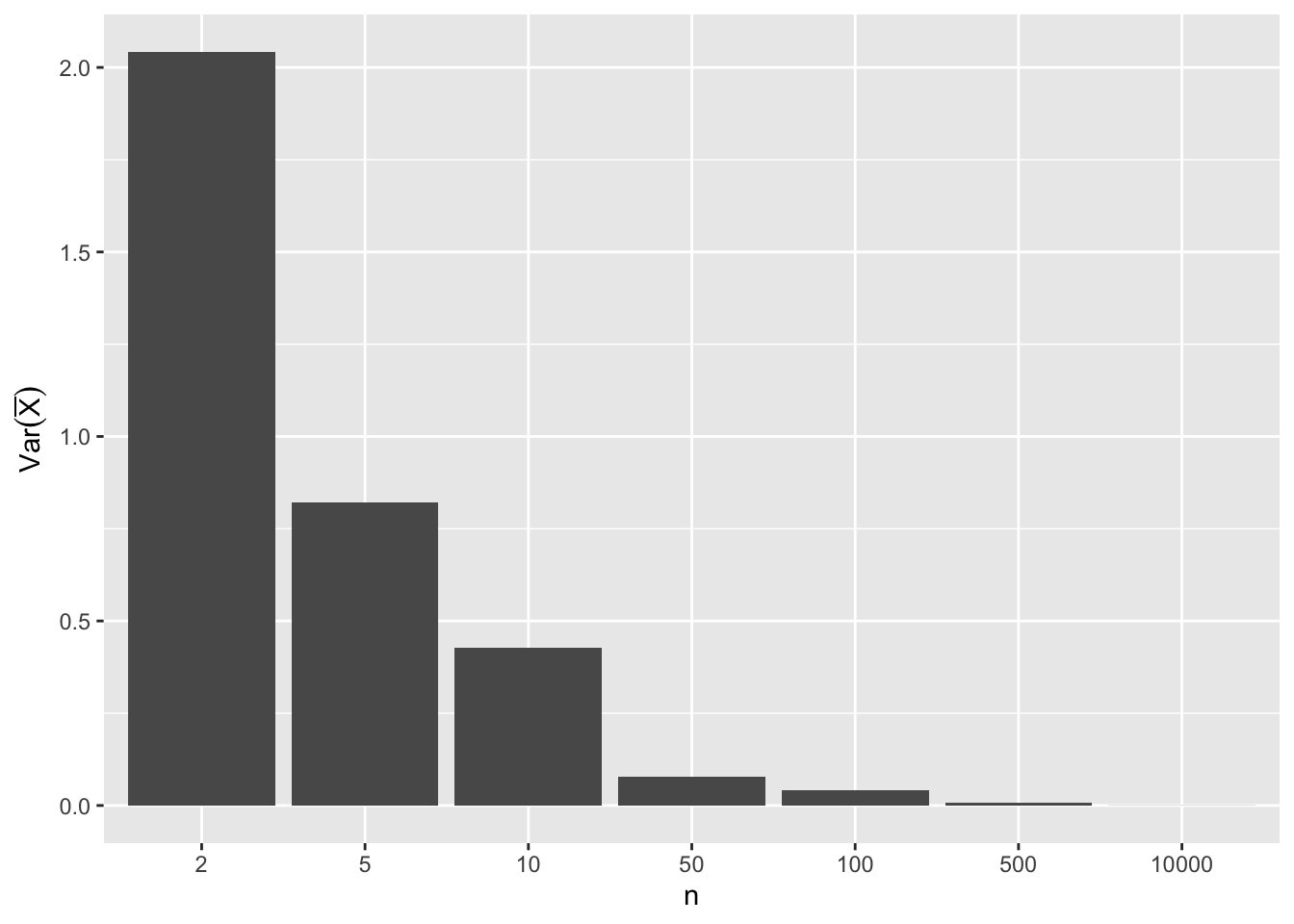
Percebemos claramente que o valor de \(Var(\bar{X})\) diminui a medida que \(n\) aumenta. Como \(\bar{X}\) é não viesado, este resultado numérico, corrobora que o estimador \(\bar{X}\) é um estimador consistente para \(\mu\).
12.7 Desafio
Sejam os estimadores \[\hat{\sigma^2} = \dfrac{\sum_{i=1}^{n}(X_i - \bar{X})^2}{n} \quad \quad \mbox{e} \quad \quad \hat{s^2} = \dfrac{\sum_{i=1}^{n}(X_i - \bar{X})^2}{n-1}.\]
Considerando a população definida neste capitulo. Verifique numericamente se os estimadores são não-viesados. Use \(n = 2\).
Considerando a população definida neste capitulo. Verifique numericamente se os estimadores são consistentes.