#Retorna o p-valor do teste unilateral a direita
p_unid2mu = function(x,y,sigma2_x,sigma2_y,mu0){
#definindo o tamanho da amostra de x
n = length(x)
#definindo o tamanho da amostra de y
m = length(y)
#Obtendo z calculado
zcal = (mean(x)-mean(y))/sqrt(sigma2_x/n+sigma2_y/m)
#calculando o p-valor
pval = pnorm(q = zcal,
mean = 0,
sd = 1,
lower.tail = FALSE)
#Retornando o p-valor
return(pval)
}21 Teste de hipóteses para a média de duas populações
Nesta seção iremos discutir o problema de se comparar a média de duas populações. A seguir abordaremos a discussão do probelma de comparar média de duas populações normais em dois cenários: populações independentes e populações dependentes.
21.1 Teste de hipóteses para comparação de médias de duas populações normais independentes com variâncias conhecidas
Vamos discutir o problema de comparar duas médias de populações normais com variâncias conhecidas. Vamos inicialmente discutir um teste unilateral a direita. As hipóteses nesse cenários seriam dadas por:
Hipótese: \[H_0: \mu_A = \mu_B \qquad \times \qquad H_1: \mu_A > \mu_B,\] ou equivalentemente, \[H_0: \mu_A - \mu_B = 0 \qquad \times \qquad H_1: \mu_A - \mu_B > 0.\]
A estatística de teste será dada por:
\[ Z = \frac{\bar{X}-\bar{Y}}{\sqrt{\frac{\sigma^2_1}{n}+\frac{\sigma^2_2}{m}}} \sim N(0,1), \]
em \(n\) é o tamanho da amostra da primeira população, \(m\) é o tamanho da amostra da segunda população, \(\sigma^2_i\) é a variância da população \(i\), \(i=1,2\), \(\bar{X}\) é a média amostral da população 1 e \(\bar{Y}\) é a média amostral da população 2.
A região crítica seria dada por:
\[ RC = \{z \in \mathbb{R}: z > k\}. \]
Ao definirmos um erro tipo I (\(\alpha\)), é possível obtermos o valor de \(k\) ou calcularmos o p-valor do teste. Vamos criar uma rotina computacional (função) que calcule o p-valor do teste definido acima.
Vamos aplicar o teste supondo que dispomos de uma amostra de 20 valores de idade de homens e 30 idades de mulheres. Sabendo-se que o desvio padrão das idades dos homens é de 2 anos e das mulheres é de 3 anos. Verifique se a idade média dos homens é maior do que a idade média das mulheres, usando um \(\alpha = 0,05\).
#Idade dos homens
idadeH = c(14, 24, 23, 13, 30, 22, 15, 23, 21, 11, 18, 19, 21, 17, 12,
18, 21, 24, 20, 22)
#Idade das mulheres
idadeM = c(6, 12, 12, 19, 17, 11, 17, 21, 17, 21, 21, 19, 14, 3, 19, 8,
15, 14, 7, 9, 14, 19, 14, 8, 12, 20, 27, 21, 14, 16)
#Calculando o p-valor do teste unilateral a direita
p_unid2mu(x = idadeH,
y = idadeM,
sigma2_x = 4,
sigma2_y = 9,
mu0 = 0)[1] 9.830802e-11Qual a conclusão?
21.2 Teste de hipóteses para comparação de médias de duas populações normais independentes com variâncias desconhecidas
Para discutir o teste de hipóteses para comparar médias de duas populações normais independentes com variâncias desconhecidas, vamos voltar ao problema discutido no Capítulo anterior.
O dono de uma fábrica, possui duas máquinas empacotando um determinado produto K. O dono da fábrica coletou a informação do peso de 25 pacotes produzidos pela máquina A e 20 pacotes produzidos pela máquina B. O produtor quer saber se as máquinas estão produzindo da mesma forma, ou seja, se as médias dos pesos dos pacotes produzidos pelas máquinas são iguais. Só que para respondermos esta pergunta, precisamos inicialmente verificar se a variância do peso dos pacotes produzidos pelas máquinas são iguais ou diferentes.
O dono da fábrica deseja saber se os pesos médios dos pacotes produzidos pelas máquinas são iguais. Com base nos dados, qual a sua conclusão?
Para responder o questionamento feito, precisamos discutir o problema de se comparar duas médias de populações normais independentes. Traduzindo em hipóteses, podemos escrever
Hipótese: \[H_0: \mu_A = \mu_B \qquad \times \qquad H_1: \mu_A \neq \mu_B,\] ou equivalentemente, \[H_0: \mu_A - \mu_B = 0 \qquad \times \qquad H_1: \mu_A - \mu_B \neq 0.\]
Para testar as hipóteses acima, precisamos nos lembrar que estamos comparando médias de duas populações normais. Entretanto, já verificamos que a suposição de normalidade dos dados é satisfeita por meio do teste de Kolmogorov Smirnov.
Existem duas estatísticas de teste para as hipóteses especificadas acima. A primeira, quando assumimos variâncias desconhecidas e iguais:
\[ T = \frac{\bar{X}-\bar{Y}}{S_p\sqrt{\frac{1}{n}+\frac{1}{m}}} \sim t_{(n+m-2)}, \]
em \(n\) é o tamanho da amostra da primeira população, \(m\) é o tamanho da amostra da segunda população, \(S_p\) é o estimador para \(\sigma^2\), conhecido como \(S\) pooled, \(\bar{X}\) é a média amostral da população 1 e \(\bar{Y}\) é a média amostral da população 2.
A segunda, quando assumimos variâncias desconhecidas e desiguais:
\[ T = \frac{\bar{X}-\bar{Y}}{\sqrt{\frac{S_1^2}{n}+\frac{S_2^2}{m}}} \sim t_{\nu} \]
em \(n\) é o tamanho da amostra da primeira população, \(m\) é o tamanho da amostra da segunda população, \(S_i\) é o estimador para \(\sigma^2_i\), \(i=1,2\), \(\bar{X}\) é a média amostral da população 1, \(\bar{Y}\) é a média amostral da população 2 e
\[ \nu = \frac{(A+B)^2}{A^2/(n-1)+B^2/(m-1)}, \]
e \(A = s^2_1/n\) e \(B = s^2/m\).
Atividade 1: Importem o arquivo Maquinas.txt e armazenem em um objeto chamado base.
#Visualizando o objeto
base# A tibble: 45 × 3
Maquina Peso Defeito
<chr> <dbl> <dbl>
1 A 107. 0
2 B 144. 0
3 A 97.8 1
4 B 137. 0
5 A 101. 0
6 A 94.5 0
7 B 134. 1
8 A 99.9 0
9 A 94.4 0
10 B 141. 1
# ℹ 35 more rowsPara executarmos o teste de comparações de médias de duas populações, usaremos a função t.test.
A seguir, vamos apresentar os principais argumentos da função t.test:
- x - o vetor com a amostra da população 1;
- y - o vetor com a amostra da população 2;
- mu - o valor do parâmetro que definem as hipóteses (default = 0);
- alternative - argumento que define se o teste é bilateral ou unilateral a esquerda e a direita (default = bilateral - two.sided);
- var.equal - argumento lógico que indica se as variâncias são iguais ou diferentes (default = FALSE);
- paired - argumento lógico que indica se o teste é para médida de populações dependentes (default = FALSE).
#Obtendo algumas medidas descritivas
resultados = base |>
group_by(Maquina) |>
summarise(N = n(),
media = mean(Peso),
desvio.padrao = sd(Peso))
resultados# A tibble: 2 × 4
Maquina N media desvio.padrao
<chr> <int> <dbl> <dbl>
1 A 25 99.6 3.11
2 B 20 141. 3.57#Visualizando graficamente o comportamento dos pesos nas duas máquinas
library(ggplot2)
#Plotando o boxplot
ggplot(data = base, aes(y = Peso, x = Maquina)) +
geom_boxplot() +
theme_minimal() +
theme_minimal()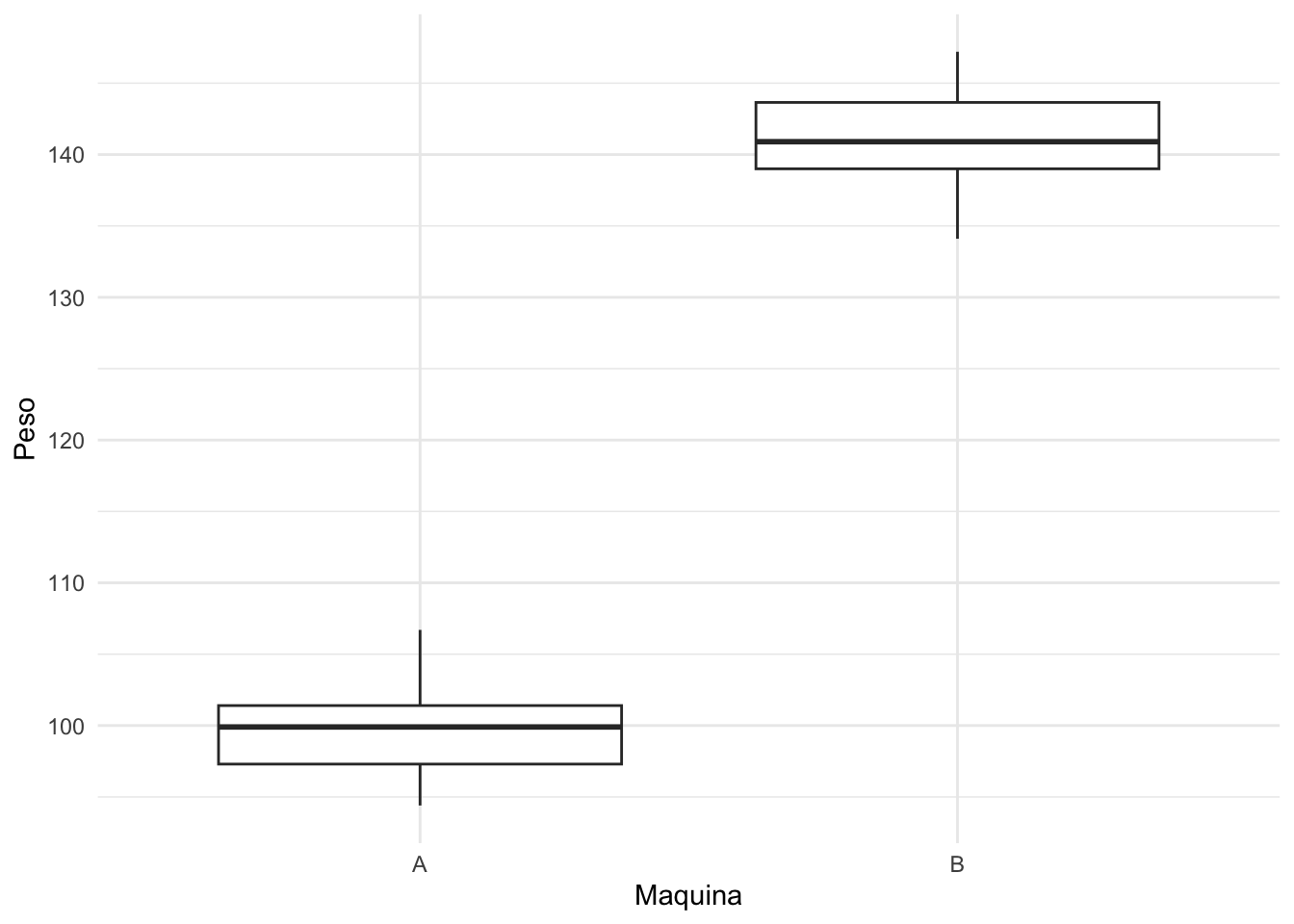
#Criando um tibble somente com as informações da máquina A
pesoA = base |>
filter(Maquina == "A")
#Criando um tibble somente com as informações da máquina B
pesoB = base |>
filter(Maquina == "B")
#Realizando o teste de médias
t.test(x = pesoA$Peso,
y = pesoB$Peso,
alternative = "two.sided",
mu = 0,
var.equal = TRUE,
conf.level = 0.95)
Two Sample t-test
data: pesoA$Peso and pesoB$Peso
t = -41.465, df = 43, p-value < 2.2e-16
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-43.29611 -39.27989
sample estimates:
mean of x mean of y
99.572 140.860 A saída do teste contém várias informações: o valor da estatística do teste \(t\), o número de graus de liberdade da estatística de teste \(df\) e o p-valor associado as hipóteses especificadas. Ele deixa explícito qual a hipótese alternativa “true difference in means is not equal to 0” que significa “a verdadeira diferença entre as médias não é 0”. Fornece também um intervalo de confiança para \(\mu_A - \mu_B\) e o valor de uma estimativa pontual para cada média.
Note que, graficamente os comportamentos dos boxplots parecem indicar que os pesos possuem comportamentos distintos. O que é ratificado pelas estimativas pontuais obtidas do peso de cada máquina. Para verificarmos a afirmação feita, precisamos realizar o teste de hipóteses. Com base em um nível de significância de 5%, rejeitamos \(H_0\) (p-valor < 0,0001 < 0,05 = \(\alpha\) ), encontramos evidências para acreditar que os pesos médios dos pacotes são diferentes nas duas máquinas.
É possível obter os intervalos de confiança para cada uma das médias como visto em aulas passadas.
#Carregando o pacote
library(Publish)Loading required package: prodlim#Calculando o intervalo de confiança para o peso do pacote por máquina
res = ci.mean(x = Peso ~ Maquina,
alpha = 0.05,
na.rm = TRUE,
data = base)
#Visualizando o objeto res
plot(x = res,
title.labels = "Sexo")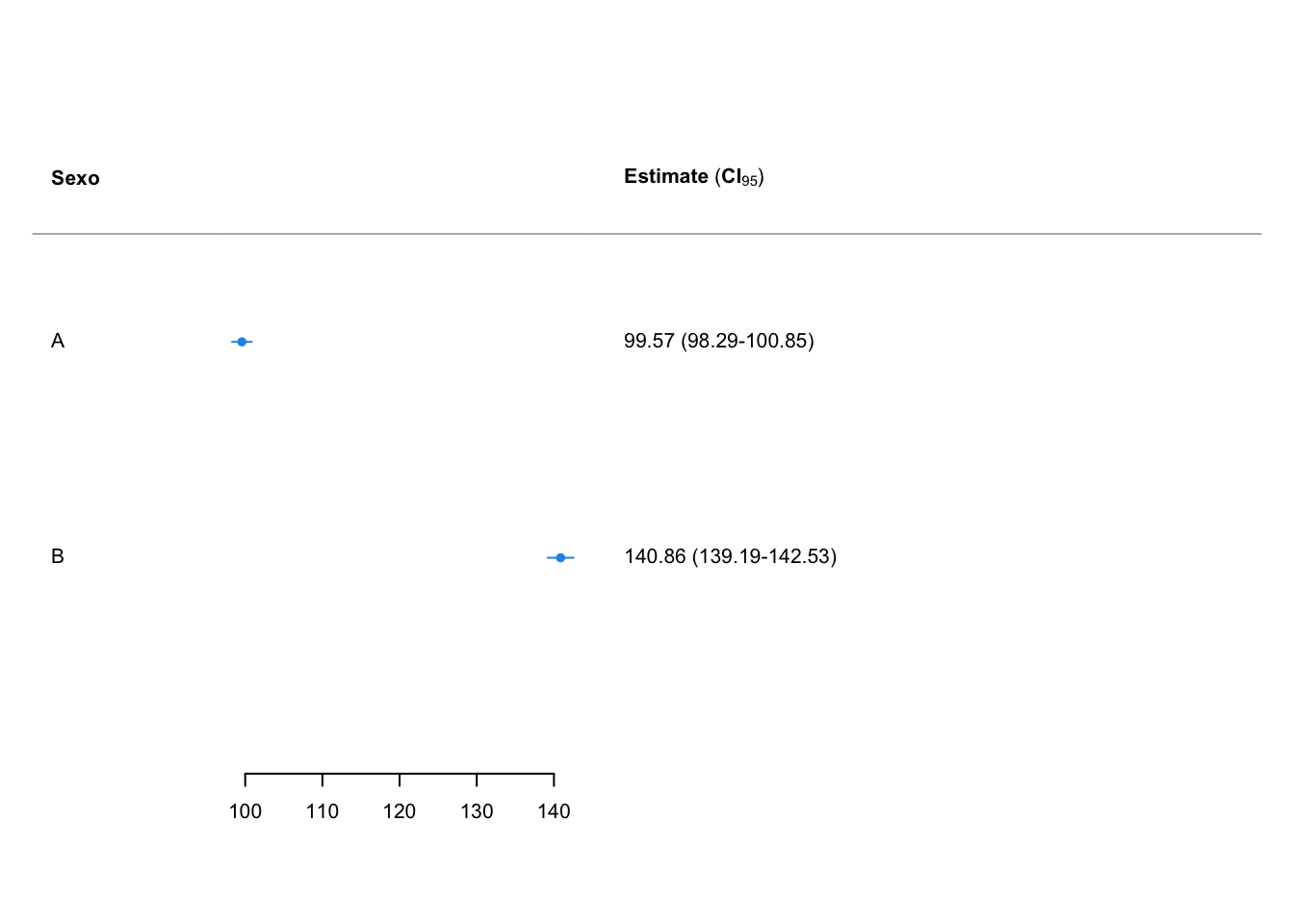
#Visualizando o objeto res
res Maquina mean CI-95%
A 99.57 [98.29;100.85]
B 140.86 [139.19;142.53]21.3 Teste de hipóteses para comparação de médias de duas populações normais dependentes
Um médico está verificando a eficácia de uma medicação para diabetis. Ele mediu a glicemia de pacientes com diabetis antes do início do tratamento e após o tratamento com a medicação. Para que o medicamento seja eficiente, o médico espera que a glicemia dos pacientes tenha diminuído. Você diria que o medicamento é eficiente?
Para responder o questionamento feito, precisamos discutir o problema de se comparar duas médias de populações normais dependentes. Traduzindo em hipóteses, podemos escrever
Hipótese: \[H_0: \mu_1 = \mu_2 \qquad \times \qquad H_1: \mu_1 > \mu_2,\] ou equivalentemente, \[H_0: \mu_1 - \mu_2 = 0 \qquad \times \qquad H_1: \mu_1 - \mu_2 > 0.\]
Para testar as hipóteses acima, precisamos nos lembrar que estamos comparando médias de duas populações normais e precisamos checar normalidade dos dados em cada população.
#Importando os dados
glicemia = read_csv2("Glicemia.csv")#Ativando pacote
library(ggpubr)
library(patchwork)
#Criando um qq-plot com o ggpubr para a população 1
qq1 = ggqqplot(glicemia$Glicemia1)
#Criando um qq-plot com o ggpubr para a população 2
qq2 = ggqqplot(glicemia$Glicemia2)
#Plotando os qqplots
qq1 + qq2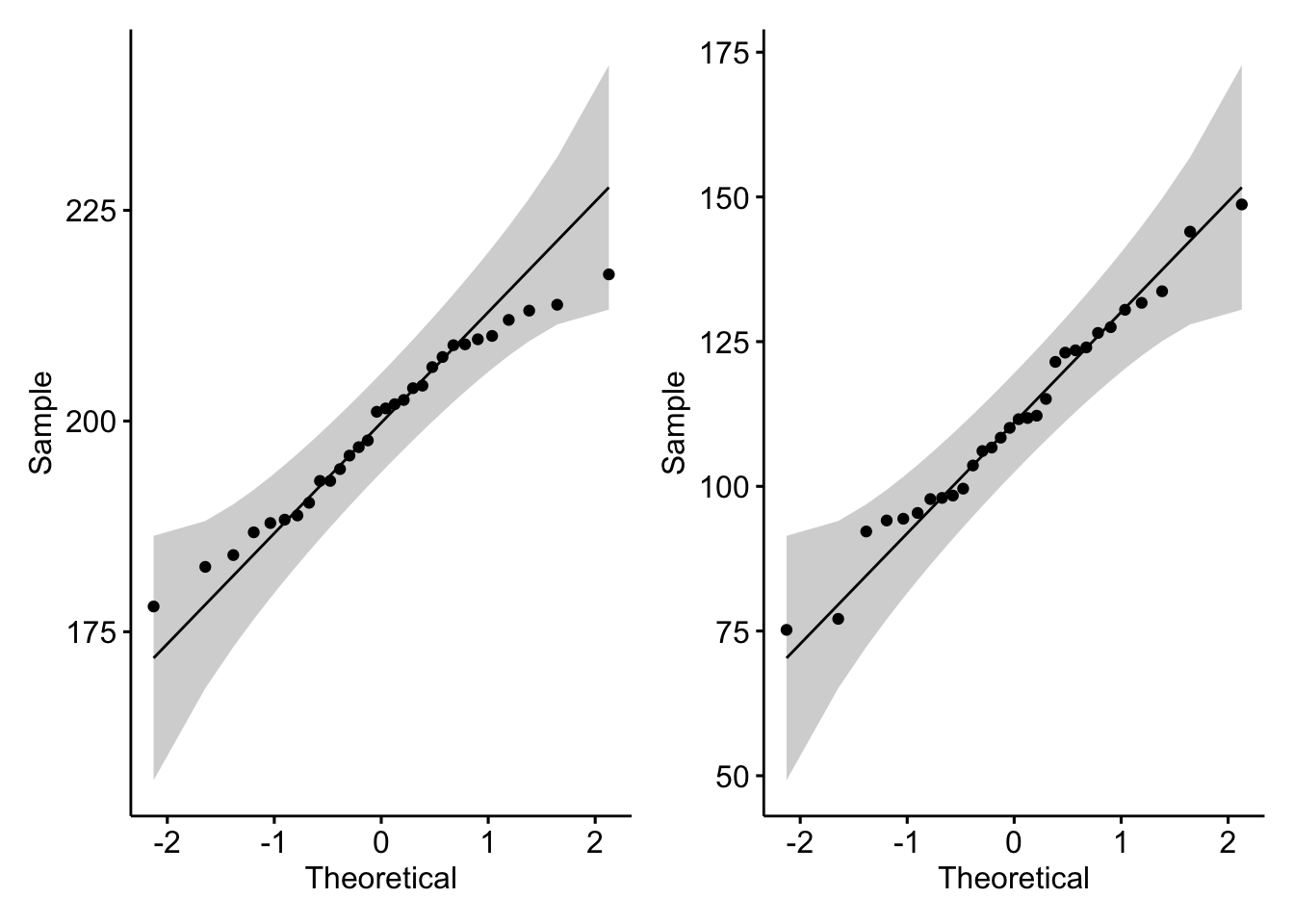
#Teste de normalidade para a população 1
shapiro.test(x = glicemia$Glicemia1)
Shapiro-Wilk normality test
data: glicemia$Glicemia1
W = 0.97001, p-value = 0.5395#Teste de normalidade para a população 2
shapiro.test(x = glicemia$Glicemia2)
Shapiro-Wilk normality test
data: glicemia$Glicemia2
W = 0.98095, p-value = 0.8503Analisando os qq-plots e os testes de normalidade, é razoável assumirmos normalidade das glicemias nos dois períodos.
#Ativando pacote
library(tidyr)
#Criando um objeto com os dados empilhados
base.mod = glicemia |>
gather(key = Tratamento,
value = Glicemia, Glicemia1, Glicemia2)
#Visualizando o novo objeto
base.mod# A tibble: 60 × 2
Tratamento Glicemia
<chr> <dbl>
1 Glicemia1 184.
2 Glicemia1 193.
3 Glicemia1 202
4 Glicemia1 188.
5 Glicemia1 204.
6 Glicemia1 198.
7 Glicemia1 187.
8 Glicemia1 197.
9 Glicemia1 189.
10 Glicemia1 210.
# ℹ 50 more rows#Obtendo medidas descritivas
resultados3 = base.mod |>
group_by(Tratamento) |>
summarise(media = mean(Glicemia),
desvio.padrao = sd(Glicemia),
N = n())
resultados3# A tibble: 2 × 4
Tratamento media desvio.padrao N
<chr> <dbl> <dbl> <int>
1 Glicemia1 199. 10.5 30
2 Glicemia2 111. 17.9 30#Plotando o boxplot
ggplot(base.mod, aes(y = Glicemia, x = Tratamento)) +
geom_boxplot() +
theme_minimal()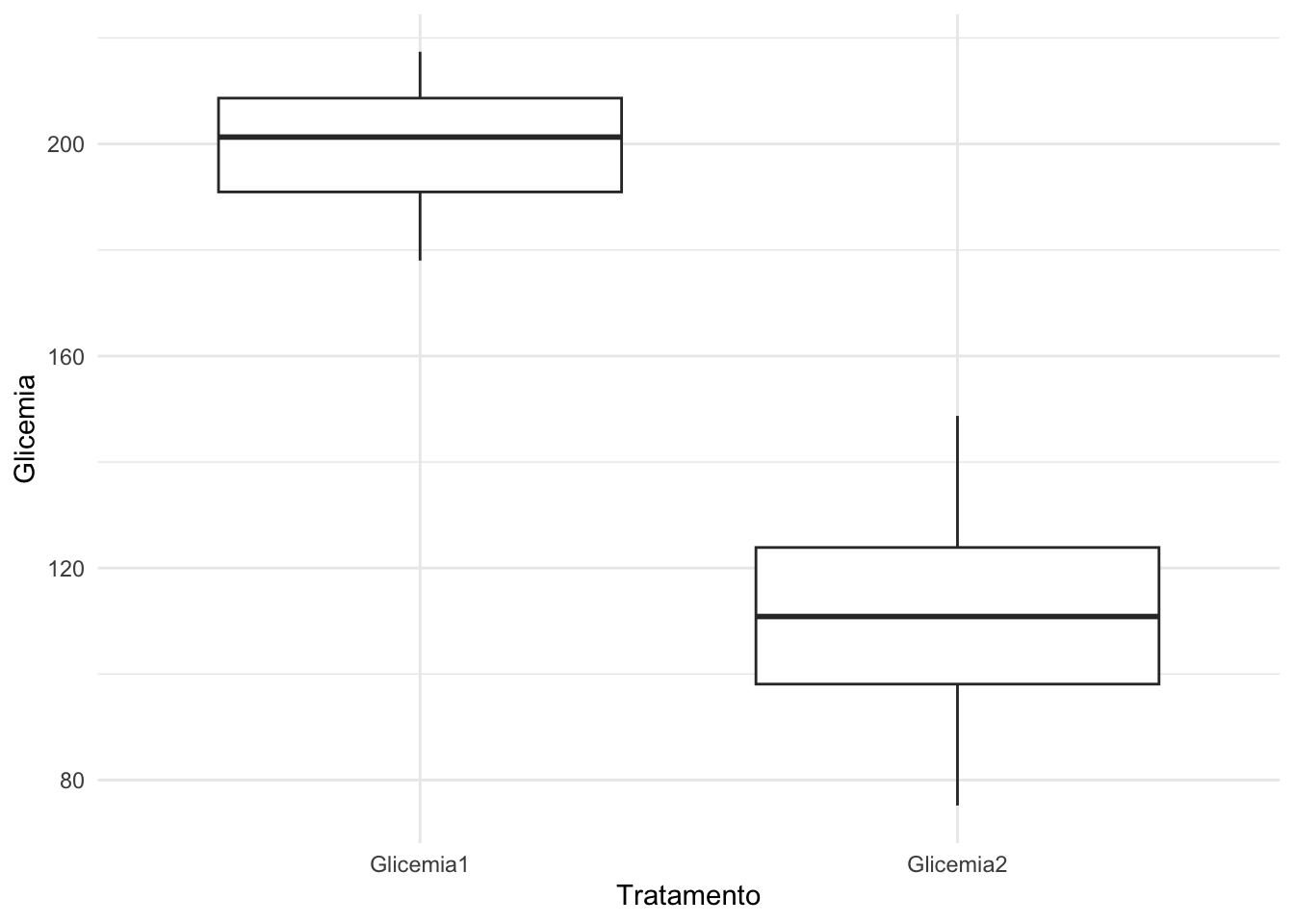
#Realizando o teste de comparação de médias de populações dependentes
t.test(x = glicemia$Glicemia1,
y = glicemia$Glicemia2,
alternative = "greater",
mu = 0,
paired = TRUE,
conf.level = 0.95)
Paired t-test
data: glicemia$Glicemia1 and glicemia$Glicemia2
t = 21.243, df = 29, p-value < 2.2e-16
alternative hypothesis: true mean difference is greater than 0
95 percent confidence interval:
80.91215 Inf
sample estimates:
mean difference
87.94667 A saída do teste informa que é um teste pareado, o mesmo é realizado sempre que informamos o argumento paired como TRUE.
Com base em um nível de significância de 5%, rejeitamos \(H_0\), indicando que possuímos evidências suficiente para acreditar que a média da glicemia após o tratamento é inferiror à média da glicemia antes do tratamento.
Realizar um teste de comparações de médias de duas populações dependentes é equivalente a realizar o teste de média de uma população para a diferença das variáveis. Veja os resultados abaixo e compare com os obtidos no passo anterior.
#Criando a variável diferença das glicemias
dif = glicemia$Glicemia1 - glicemia$Glicemia2
#Realizando o teste de média de uma população
t.test(x = dif,
alternative = "greater",
mu = 0,
conf.level = 0.95)
One Sample t-test
data: dif
t = 21.243, df = 29, p-value < 2.2e-16
alternative hypothesis: true mean is greater than 0
95 percent confidence interval:
80.91215 Inf
sample estimates:
mean of x
87.94667 21.4 Desafio
Utilize a base Dados socio.txt para responder as perguntas de 1 a 3.
Com base em um nível de significância de 5%, você diria que as idades médias de homens e mulheres são diferentes?
Com base em um nível de significância de 1%, você diria que os pesos médios de homens e mulheres são iguais?
Com base em um nível de significância de 5%, você diria que a satisfação média dos homens é maior do que a satisfação média das mulheres?
Crie uma função que calcula o p-valor para o teste bilateral de comparação de médias de duas populações normais com variâncias conhecidas independentes.
Crie uma função que calcula o p-valor para o teste bilateral de comparação de médias de duas populações normais com variâncias conhecidas dependentes.