#Ativando pacote
library(animation)
#Construindo 50 IC para mu com 95%
conf.int(level = .95,
size = 50)13 Estimativas intervalares
Ao conduzir uma análise estatística, frequentemente buscamos estimar parâmetros desconhecidos de interesse. Por exemplo, ao estudar a renda dos residentes de Niterói com mais de 18 anos, definimos:
População: residentes de Niterói com mais de 18 anos.
Variável: a renda (em reais) do morador.
Parâmetro de interesse: renda média dos moradores maiores de 18 anos de Niterói.
Oferecer apenas uma estimativa pontual da renda média pode ser limitado em termos informativos. Para uma análise mais abrangente, é aconselhável fornecer uma estimativa intervalar por meio de um intervalo de confiança.
13.1 IC para a média de uma população normal com variância conhecida
Considere uma amostra aleatória simples \(X_1, \ldots, X_n\) obtida de uma população normal com média \(\mu\) e variância \(\sigma^2\) conhecida.
Como \(\bar{X}\) é uma combinação linear de variáveis aleatórias normais, então \[\bar{X} \sim N\left( \mu, \frac{\sigma^2}{n} \right).\]
Sendo assim, ao padronizarmos a distribuição de \(\bar{X}\) temos que \[Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \sim N(0,1).\]
Então, podemos escrever que
\[\begin{equation} P(z_{\alpha/2} \leq Z \leq z_{1-\alpha/2}) = 1 - \alpha, \end{equation}\]em que \(z_{\alpha/2}\) e \(z_{1-\alpha/2}\) são quantis da distribuição normal padrão, cuja área entre eles é de \(1-\alpha\). Além disso, a área abaixo de \(z_{\alpha/2}\) é de \(\alpha/2\) e de \(z_{1-\alpha/2}\) é \(1 - \alpha/2\), como está representado na figura abaixo.
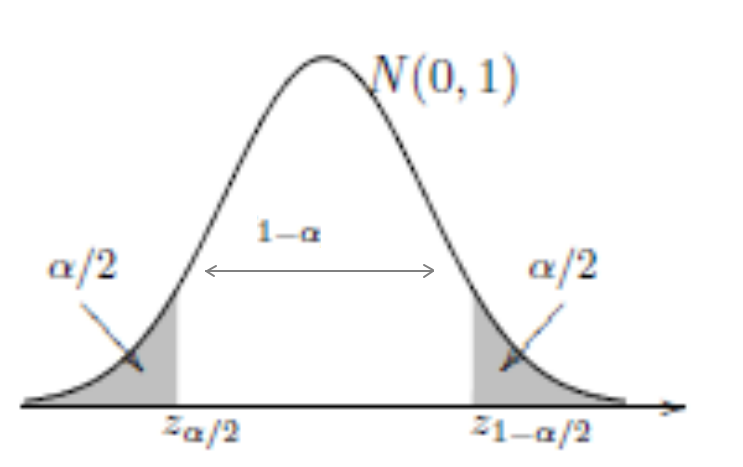
Como \(Z = \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\) tem distribuição normal padrão, podemos reescrever a Equação acima da seguinte forma \[P\left(z_{\alpha/2} \leq \frac{\bar{X}-\mu}{\sigma/\sqrt{n}} \leq z_{1-\alpha/2}\right) = 1 - \alpha,\] com algumas operações algébricas conseguimos \[P\left(\bar{X} - z_{\alpha/2} \frac{\sigma}{\sqrt{n}} \leq \mu \leq \bar{X} + z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \right) = 1 - \alpha.\] Devemos notar que na equação acima, as extremidades é que são aleatórias, daí temos que \[IC(\mu, 1-\alpha) = \left(\bar{X} - z_{\alpha/2} \frac{\sigma}{\sqrt{n}} ; \bar{X} + z_{1-\alpha/2} \frac{\sigma}{\sqrt{n}} \right)\]
Como interpretar o IC obtido acima?
Como o que é aleatório é o intervalo, interpretamos o mesmo da seguinte forma: se fossem construídos 100 intervalos com amostras de mesmo tamanho, \(100(1−\alpha)\) intervalos aproximadamente conteriam o verdadeiro valor da média \(\mu\), isto é, existe \(100(1−\alpha)\%\) de chance do intervalo conter a verdadeira média populacional.
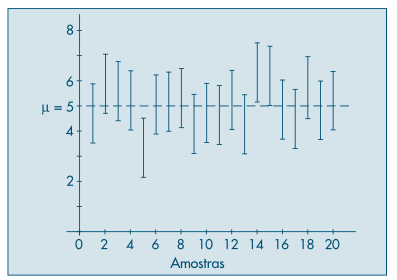
A Figura acima, retirada do Morettin e Bussab (2006), exemplifica o que foi dito. Nela temos 20 intervalos de confiança para \(\mu\), todos de tamanho \(n\), com \(90\%\) de confiança. Deste modo, esperamos que em torno de \(90\%\) dos intervalos contenham o valor de \(\mu = 5\), isto é, que 18 intervalos contenham este valor.
Observação: NÃO existe a interpretação (um tanto comum de se ouvir) que a prababilidade da média estar no intervalo de confiança é de \(1 - \alpha\) . E por que não faz sentido isso? Veja que o intervalo construído ou contém ou não contém a média, porque o parâmetro de interesse é uma constante desconhecida, ou seja, ou o intervalo conterá esse valor ou não.
A função conf.int, do pacote animation, cria uma animação para demonstrar o conceito de intervalo de confiança. No exemplo dado abaixo, gera 50 amostras de uma distribuição normal padrão \(N(\mu = 0, \sigma^2 = 1)\) e calcula o IC para a média de cada amostra. Ela exibe o coverage rate, que representa o nível de confiança. Vale ressaltar que como estamos realizando o sorteio de aostras aleatórias, eseramos que o coverage rate encontro valores próximos ao nível de significância especificado.
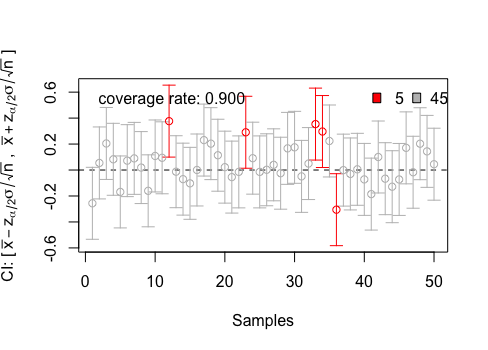
Vamos desenvolver uma função em R que recebe um vetor numérico como entrada e calcula o intervalo de confiança para a média de uma distribuição normal com variância populacional conhecida.
#Criando uma função que calcula o IC para a média de uma população normal com variância conhecida
IC.media = function(x, conf, sigma){
#tamanho da amostra
n = length(x)
#média amostral
x.barra = mean(x,
na.rm = TRUE)
alfa = 1 - conf
#calculando o quantil z_{1-alpha/2}
z = qnorm(p = 1 - alfa/2,
mean = 0,
sd = 1)
#calculando o limite inferior do IC com 2 casas decimais
LI = round(x.barra - z*sigma/sqrt(n),
digits = 2)
#calculando o limite inferior do IC com 2 casas decimais
LS = round(x.barra + z*sigma/sqrt(n),
digits = 2)
#organizando a mensagem a ser imprimida pela função
cat("IC(média,",conf*100,"%):[",LI,";",LS,"]", sep="")
}A seguir vamos aplicar a função criada em um conjunto de dados referentes a altura (em cm), supondo que a variância populacional \(\sigma^2 = 222 \mbox{cm}^2\).
#Carregando o pacote tidyverse
library(tibble)
#Criando um tibble com a altura (em cm) e o sexo dos indivíduos.
base = tibble(altura = c(168.5,180,173.4,200.2,197,160.5,182,195.7,158,174.6),
sexo = c("F","M","F","M","M","F","M","M","F","F"))
#Calculando o intervalo de confiança para a altura média supondo que a variância
#é de 222 cm^2 ao quadrado e que a altura possui distribuição normal
IC.media(x = base$altura,
conf = 0.95,
sigma = sqrt(222))IC(média,95%):[169.76;188.22]Interpretação: se fossem construídos 100 intervalos com amostras de mesmo tamanho, \(95\) intervalos, aproximadamente, conteriam o verdadeiro valor da altura média \(\mu\), isto é, existe \(95\%\) de chance do intervalo conter a altura média populacional.
13.2 IC para a média de uma população normal com variância desconhecida
Considere uma amostra aleatória simples \(X_1, \ldots, X_n\) obtida de uma população normal com média \(\mu\) e variância \(\sigma^2\) desconhecida. Podemos obter o intervalo de confiança para a média partindo da seguinte distribuição amostral \[T = \frac{\bar{X}-\mu}{S/\sqrt{n}} \sim t_{(n-1)},\] em que \(S\) é o desvio padrão amostral. É possível checarmos esse resultado empiricamente.
É possível derivarmos o intervalo de confiança para a média de uma população normal com variância desconhecida da distribuição acima, seguindo os passos da seção anterior. Deste modo, iremos obter \[IC(\mu, 1-\alpha) = \left(\bar{X} - t_{(n-1);\alpha/2} \frac{S}{\sqrt{n}} ; \bar{X} + t_{(n-1);1-\alpha/2} \frac{S}{\sqrt{n}} \right),\] em que em que \(t_{(n−1);\alpha/2}\) e \(t_{(n−1);1−\alpha/2}\) são quantis da distribuição \(t\) com \(n−1\) graus de liberdade cuja área entre eles é de \(1−\alpha\). Além disso, a área abaixo de \(t_{(n−1);\alpha/2}\) é \(\alpha/2\) e a área abaixo de \(t_{(n−1);1−\alpha/2}\) é \(1−\alpha/2\).
Existem diversos pacotes no R que nos permitem calcular intervalos de confiança para a média de uma população com variância desconhecida. Aqui, iremos explorar a função ci.mean do pacote Publish.
A seguir, vamos apresentar os principais argumentos da função ci.mean:
- x - o vetor com os valores da amostra;
- \(\alpha\) - o complementar do nível de confiança (default = 0.05);
- na.rm - um operador lógico indicando se deseja desconsiderar os valores faltantes (default = TRUE).
#Carregando o pacote
library(Publish)
#Calculando o intervalo de confiança para a altura média assumindo que a variância populacional é desconhecida
ci.mean(x = base$altura,
alpha = 0.05,
na.rm = TRUE) mean CI-95%
178.99 [168.31;189.67]Podemos notar que a função nos retorna uma estimativa pontual e uma estimativa intervalar com base em um nível de confiança de \(95\%\).
Suponha que você deseje calcular uma estimativa intervalar para várias subpopulações, por exemplo, calcular um intervalo de confiança para a altura média por sexo.
#Calculando o intervalo de confiança para a altura média por sexo assumindo que a variância populacional é desconhecida
res = ci.mean(x = altura ~ sexo,
alpha = 0.05,
na.rm = TRUE,
data = base)
#Visualizando o objeto res
res sexo mean CI-95%
F 167.00 [157.70;176.30]
M 190.98 [179.45;202.51]Podemos plotar as estimativas pontuais
#Visualizando o objeto res
plot(x = res,
title.labels = "Sexo")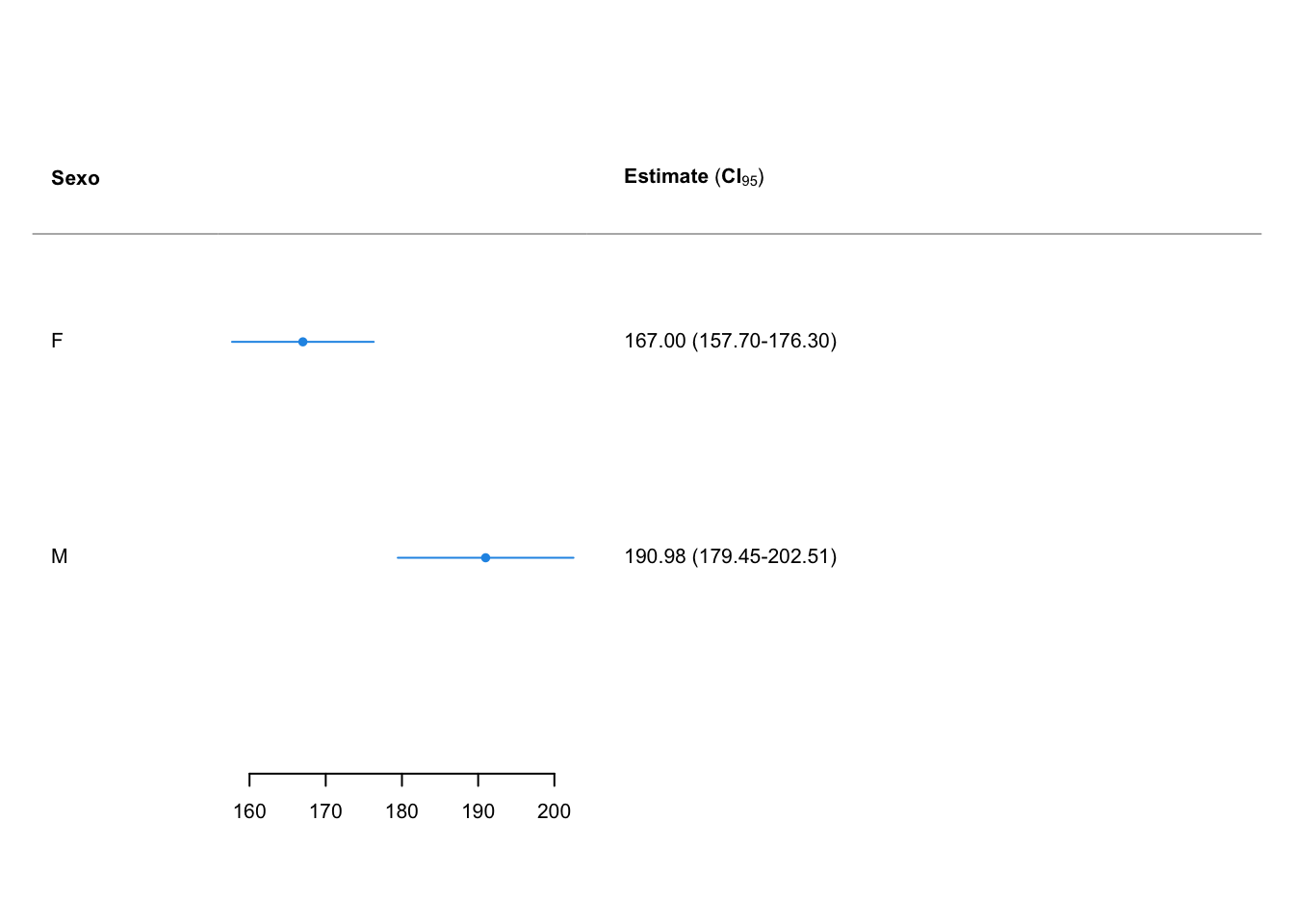
13.3 Intervalo de confiança para a proporção
Seja o intervalo de confiança para a proporção populacional dado por \[IC(p, 1-\alpha) = \left(\hat{p} - z_{\alpha/2} \sqrt{\frac{p(1-p)}{n}} ; \hat{p} + z_{1-\alpha/2} \sqrt{\frac{p(1-p)}{n}} \right).\]
O IC acima pode ser encarado sob duas abordagens: a otimista e a conservadora. Existem diversos pacotes no R que nos permitem calcular intervalos de confiança para a proporção de uma população. Aqui, iremos explorar a função binom.confint do pacote binom.
A seguir, vamos apresentar os principais argumentos da função binom.confint:
- x - o número de indivíduos com a característica de interesse;
- n - o tamanho da amostra;
- conf.level - o nível de confiança (default = 0.95);
- methods - o método a ser usado (use o método asymptotic para calcular o intervalo exibido acima).
Vamos calcular uma estimativa intervalar para a proporção de pessoas com altura superior de 180 cm na população?
#Variável que indica se o indivíduo possui mais do que 180 cm
altura_180 = c(0,0,0,1,1,0,1,1,0,0)
#Carregando o pacote binom
library(binom)
#Calculando o intervalo otmista para a proporção de pessoas com mais de 180 cm na população
binom.confint(x = sum(altura_180),
n = length(altura_180),
methods = "asymptotic") method x n mean lower upper
1 asymptotic 4 10 0.4 0.09636369 0.7036363O que podemos falar sobre a amplitude do intervalo obtido? Parece grande? Por que?
13.4 Intervalo de confiança para a variância de uma população normal
Considere uma amostra aleatória simples \(X_1, \ldots,X_n\) obtida de uma população normal com média \(\mu\) e variância \(\sigma_ 2\). Sabemos que um estimador para \(\sigma^2\) é a variância amostral \(S^2\). Sabemos também que \[Q = \frac{(n-1)S^2}{\sigma^2} \sim \chi^2_{(n-1)}.\] Então podemos escrever que \[P\left(q_{\alpha/2} \leq Q \leq q_{1-\alpha/2}\right) = 1 - \alpha,\] ou seja, \[P\left(q_{\alpha/2} \leq \frac{(n-1)S^2}{\sigma^2} \leq q_{1-\alpha/2}\right) = 1 - \alpha,\] com algumas operações algébricas conseguimos \[P\left(\frac{(n-1)S^2}{q_{1-\alpha/2}} \leq \sigma^2 \leq \frac{(n-1)S^2}{q_{\alpha/2}} \right) = 1 - \alpha.\] Temos que \[IC(\sigma^2, 1-\alpha) = \left(\frac{(n-1)S^2}{q_{1-\alpha/2}} ; \frac{(n-1)S^2}{q_{\alpha/2}} \right).\]
Existem diversos pacotes no R que nos permitem calcular intervalos de confiança para a variância de uma população normal. Aqui, iremos explorar a função VarCI do pacote DescTools.
A seguir, vamos apresentar os principais argumentos da função VarCI:
- x - um vetor com os dados;
- method - o método utilizado para calcular o intervalo (use o método classic);
- conf.level - o nível de confiança (default = 0.95).
Vamos obter uma estimativa intervalar para a variância da estatura da população (a variável se encontra no arquivo base saúde)?
#Visualizando o objeto
base_saude# A tibble: 30 × 10
Codigo Datacol Sexo Idade Peso Estatura HIV Escol DST Tipo
<chr> <chr> <dbl> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 AB01 14/10/15 1 20 61,2 1.6 1 3 1 2
2 AB02 09/02/16 0 30 60 1.55 0 5 0 NA
3 AB03 01/03/10 0 50 80 1.83 1 2 1 3
4 AB04 04/05/13 0 43 83 1.9 1 NA 1 2
5 AB05 20/05/14 0 22 75,3 1.75 0 2 1 3
6 AB06 30/01/11 1 15 70,2 1.7 1 6 0 NA
7 AB07 05/08/15 1 22 60 1.65 1 5 1 3
8 AB08 08/12/13 1 25 62 1.55 0 1 0 2
9 AB09 03/11/10 1 32 61 1.62 1 4 1 1
10 AB10 10/10/10 1 33 55 1.55 1 5 1 NA
# ℹ 20 more rows#Carregando o pacote DescTools
library(DescTools)
#Calculando o IC para a variância da Estatura (assumindo uma distribuição normal)
VarCI(x = base_saude$Estatura,
method = "classic",
conf.level = 0.97,
na.rm = TRUE) var lwr.ci upr.ci
0.011795567 0.007083579 0.023112365 13.5 Desafio
Leia o arquivo base saude.txt e salve em um objeto chamado base_saude. Sabe-se que o código 9 foi utilizado para indicar valores faltantes.
Calcule o IC par a média da variável Idade, assumindo que a variável em questão possui distribuição normal com variância 16.
Melhore a função que calcula o IC para a média, isto é, faça com que ela retorne além da estimativa intervalar para idade, também retorne uma estimativa pontual e todas as estimativas fornecidas possuam 2 casas decimais.
Crie uma função que calcula o intervalo de confiança conservador para a proporção populacional.
Leia o arquivo cafe.rds. Suponha que o peso dos cafés tem distribuição normal. Calcule o IC para o peso médio dos pacotes do café, para a variância do peso dos pacotes de café e para a proporção de pacotes com peso superior a 500 g.