15 Erro Tipo II e Função Poder

Agora vamos discutir os conceitos de erro tipo II e função poder.

15.1 Erro Tipo II para um teste de média unilateral à direita.

Considere uma amostra aleatória simples \(X_1,\ldots,X_n\) obtida de uma população normal com média \(\mu\) e variância \(\sigma^2 = 50\) (conhecida).

Suponha que desejamos testar as seguintes hipóteses sobre \(\mu\),

\[H_0: \mu = 500 \quad \times \quad H_1: \mu > 500.\] O teste acima possui uma região crítica definida por

\[RC = \{\bar{x} \in \mathbb{R}: \bar{x} \geq k\}.\]

Se desejamos calcular o Erro tipo II (chamado de \(\beta\)) associado ao teste acima, devemos calcular

\[\begin{eqnarray} \beta & = & P(\mbox{Erro Tipo II})\\ & = & P(\mbox{Não Rejeitar } H_0| H_0 \mbox{ é falsa}) \\ & = & P\left(\bar{X} \notin RC | H_0 \mbox{ é falsa} \right) \\ & = & P\left(\bar{X} < k | H_0 \mbox{ é falsa}\right) \\ \end{eqnarray}\]

Para resolvermos a probabilidade acima é necessário conhecer \(k\), mas este só será conhecido se fixarmos um valor para \(\alpha\) = P(Erro Tipo I), por exemplo, vamos definí-lo como 0,05:

\[\begin{eqnarray} \alpha & = & P(\mbox{Erro Tipo I})\\ & = & P(\mbox{Rejeitar } H_0| H_0 \mbox{ é verdadeira}) \\ & = & P\left(\bar{X} \in RC | H_0 \mbox{ é verdadeira} \right) \\ & = & P\left(\bar{X} \geq k | \bar{X} \sim N\left(500, \frac{50}{24}\right) \right) = 0,05 \\ \end{eqnarray}\]

Deste modo é possível definir o valor de \(k\), basta encontrarmos o quantil da distribuição de \(\bar{X}\) que deixa uma área acima dele de \(0,05\), isto é, \(k(\alpha)\).

Definido o valor de \(k\), podemos calcular \(\beta\)?

Note que só é possível calcularmos \(\beta\) se conhecermos a distribuição de probabilidade de \(\bar{X}\). A mesma só será conhecida se definirmos um valor para \(\mu\), então \(\beta\) é uma função de \(\mu\), logo, podemos escrever:

\[\begin{eqnarray} \beta(\mu) & = & P(\mbox{Erro Tipo II})\\ & = & P(\mbox{Não Rejeitar } H_0| H_0 \mbox{ é falsa}) \\ & = & P(\mbox{Não Rejeitar } H_0| \mu) \\ & = & P\left(\bar{X} \notin RC | \mu \right) \\ & = & P\left(\bar{X} < k | \bar{X} \sim N\left(\mu, \frac{50}{24}\right)\right) \\ \end{eqnarray}\]

Com base nas equações desenvolvidas acima, podemos criar uma rotina computacional (uma função) que receberá como argumentos: tamanho da amostra (\(n\)), nível de significância (alfa), valor da média a ser testado (mu0), valor da variância populacional (sigma2) e o valor da média na qual será calculado o valor do erro tipo II (mu).

#Criando uma função que calcula o erro tipo II para um teste de hipóteses
#unilateral a direita da média de uma população normal com variância conhecida
erroII_unid = function(n,alfa,mu,mu0,sigma2){
  k = qnorm(p = alfa,
            mean = mu0,
            sd = sqrt(sigma2/n),
            lower.tail = FALSE)
  beta = pnorm(q = k, 
               mean = mu, 
               sd = sqrt(sigma2/n))
  return(beta)
}

Suponha que foi observada uma amostra de 24 valores, qual será o erro tipo II do teste se \(\mu =\) 504?

#Calculando o erro tipo II para mu = 504
erroII_unid(n = 24,
             alfa = 0.05, 
             mu = 504, 
             mu0 = 500,
             sigma2 = 50)

[1] 0.1299923

Notamos que a probabilidade de afirmarmos que a média é 500 (não rejeitar \(H_0\)) quando na verdade ela é 504 é de aproximadamente 12,99% aproximadamente, ou seja, a probabilidade do teste cometer esse erro é baixa.

Como podemos obter esta probabilidade para diversos valores de \(\mu\)? Vamos plotar a função criada para valores de \(\mu\) de 490 a 520?

#Carregando pacote
library(ggplot2)
library(tibble)

#Plotando a função do erro tipo II
ggplot(data = tibble(val = c(490,520)), 
       mapping = aes(x = val)) +
  stat_function(fun = erroII_unid,
                args = list(n = 24,
                            alfa = 0.05,
                            mu0 = 500,
                            sigma2 = 50)) +
  xlab(expression(mu)) +
  ylab(expression(beta(mu))) +
  theme_minimal() +
  scale_x_continuous(breaks = seq(490, 520, 2))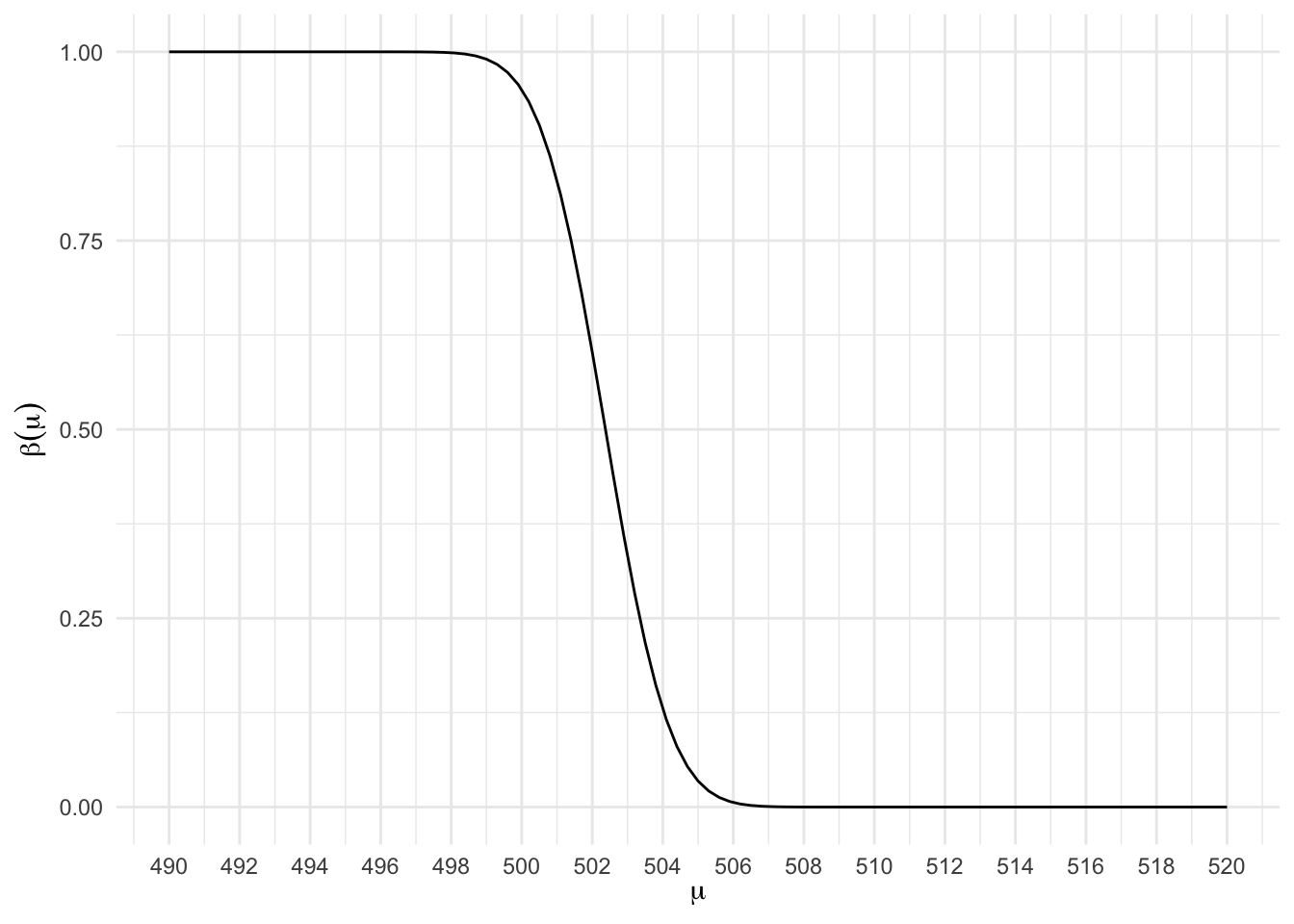

Percebemos que quanto maior for o valor da verdadeira média da população, \(\mu\), menor será a probabilidade do teste cometer o erro tipo II, isto é, menor é a probabilidade do teste dizer que a média é 500, quando na verdade ela é maior do que 500. Mais do que isso, em cenários mais fáceis, a probabilidade do erro é menor.

Seria possível definir a região crítica de forma diferente? Sim!

Ao invés de tomarmos a decisão usando \(\bar{x}\), podemos tomar a decisão com base em uma transformação de \(\bar{x}\), isto é, podemos tomar decisão com base em:

\[ Z = \frac{\bar{X}-\mu}{\frac{\sigma}{\sqrt{n}}}. \]

A região crítica seria definida por:

\[RC = \{z \in \mathbb{R}: z \geq c\}.\]

Veja que para obtermos o limiar da região crítica (\(c\)), como \(H_0\) é verdadeira, a distribuição \(Z\) estará centrada no \(E(Z) = 0\). Já para calcularmos o erro tipo II, a distribuição de \(Z\) estará centrada em \(E(Z) = (\mu-\mu_0)/\frac{\sigma}{\sqrt{n}}\). Em ambos os casos a variância é igual a 1. Deste modo, podemos definir uma rotina computacional para obter o erro tipo II com base na distribuição de \(Z\) e não em \(\bar{X}\).

#Criando uma função que calcula o erro tipo II para um teste de hipóteses
#unilateral a direita da média de uma população normal com variância conhecida
#usando a distribuição z e não de x.barra
erroII_unidZ = function(n,alfa,mu,mu0,sigma2){
  c = qnorm(p = alfa,
            mean = 0,
            sd = 1,
            lower.tail = FALSE)
  beta = pnorm(q = c, 
               mean = (mu-mu0)/sqrt(sigma2/n), 
               sd = 1)
  return(beta)
}

Vamos aplicar a nova função no mesmo cenário avaliado anteriormente.

Lembrando que sob \(H_0\), \(Z \sim N(0,1)\) e sob \(H_1\) \(Z \sim N\left((504-500)/\sqrt{\frac{50}{24}},1\right)\).

#Calculando o erro tipo II usando a distribuição de z
erroII_unidZ(n = 24,
             alfa = 0.05, 
             mu = 504, 
             mu0 = 500,
             sigma2 = 50)

[1] 0.1299923

Abaixo, temos em vermelho a distribuição sob \(H_0\). Já a distibuição em azul é sob \(H_1\) (\(\mu\)). As distribuições estão na escala padronizada \(Z\).

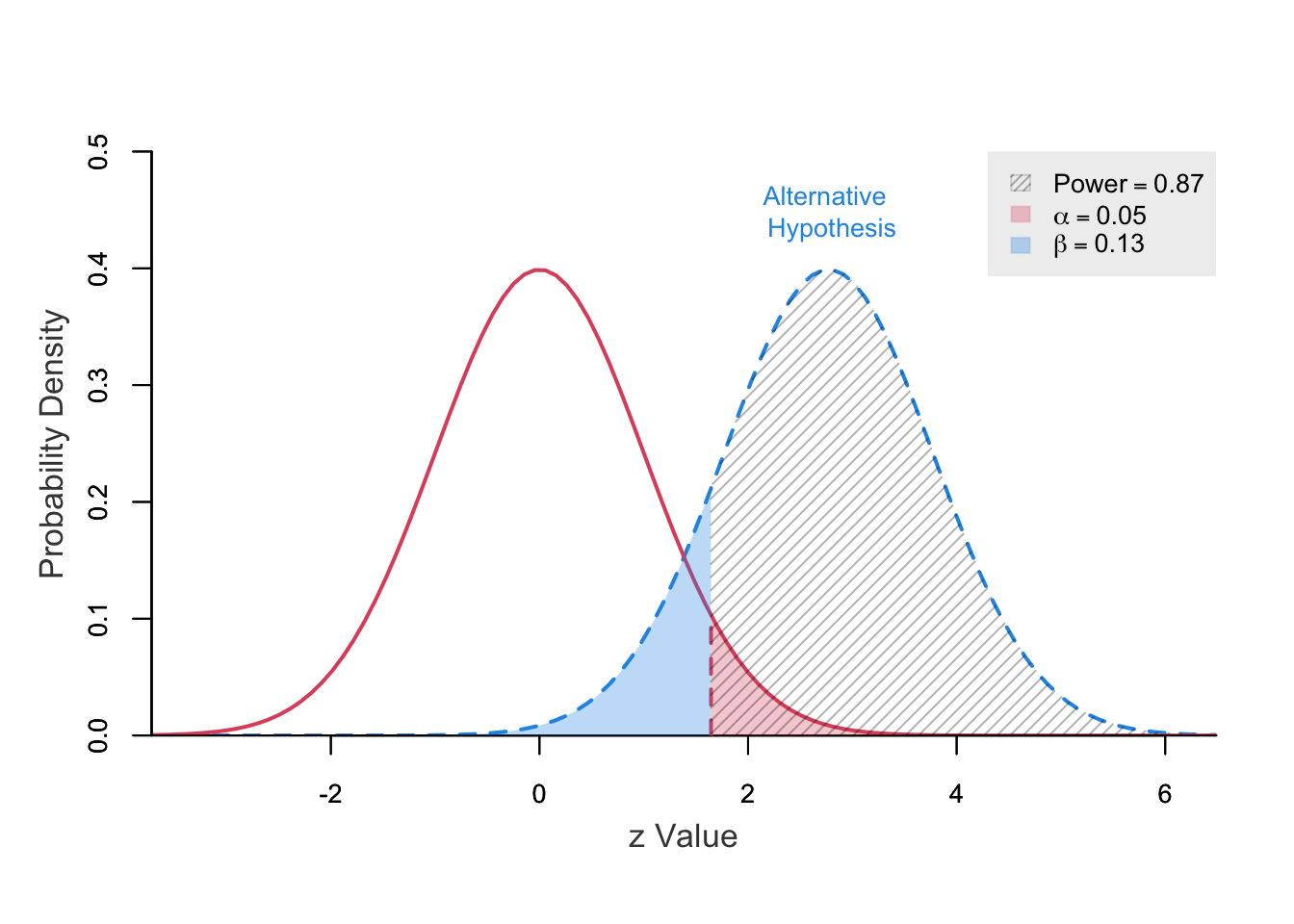
O erro tipo I é a área em vermelho acima de \(c%\) na distribuição sob \(H_0\) (0,05) e o erro tipo II é a área em azul abaixo de \(c\) na distribuição sob a hipótese alternativa (0,13). O significado da área hachurada será discutida mais a frente.

15.1.1 Efeito do tamanho da amostra no erro tipo II

Se ao invés de obervarmos uma amostra de tamanho 24, nós tivessemos observados uma amostra de tamanho 50, qual seria o comportamento da função do erro tipo II, ele mudaria?

#Plotando a função do erro tipo II
ggplot(data = tibble(val = c(490,520)), aes(x = val)) +
  stat_function(mapping = aes(colour = "24"),
                fun = erroII_unid,
                args = list(n = 24,
                            alfa = 0.05,
                            mu0 = 500,
                            sigma2 = 50)) +
  stat_function(mapping = aes(colour = "50"),
                fun = erroII_unid,
                args = list(n = 50,
                            alfa = 0.05,
                            mu0 = 500,
                            sigma2 = 50)) +
  xlab(expression(mu)) +
  ylab(expression(beta(mu))) +
  scale_colour_manual("n", values = c("Black", "Red")) +
  theme_minimal() +
  scale_x_continuous(breaks = seq(490, 520, 2))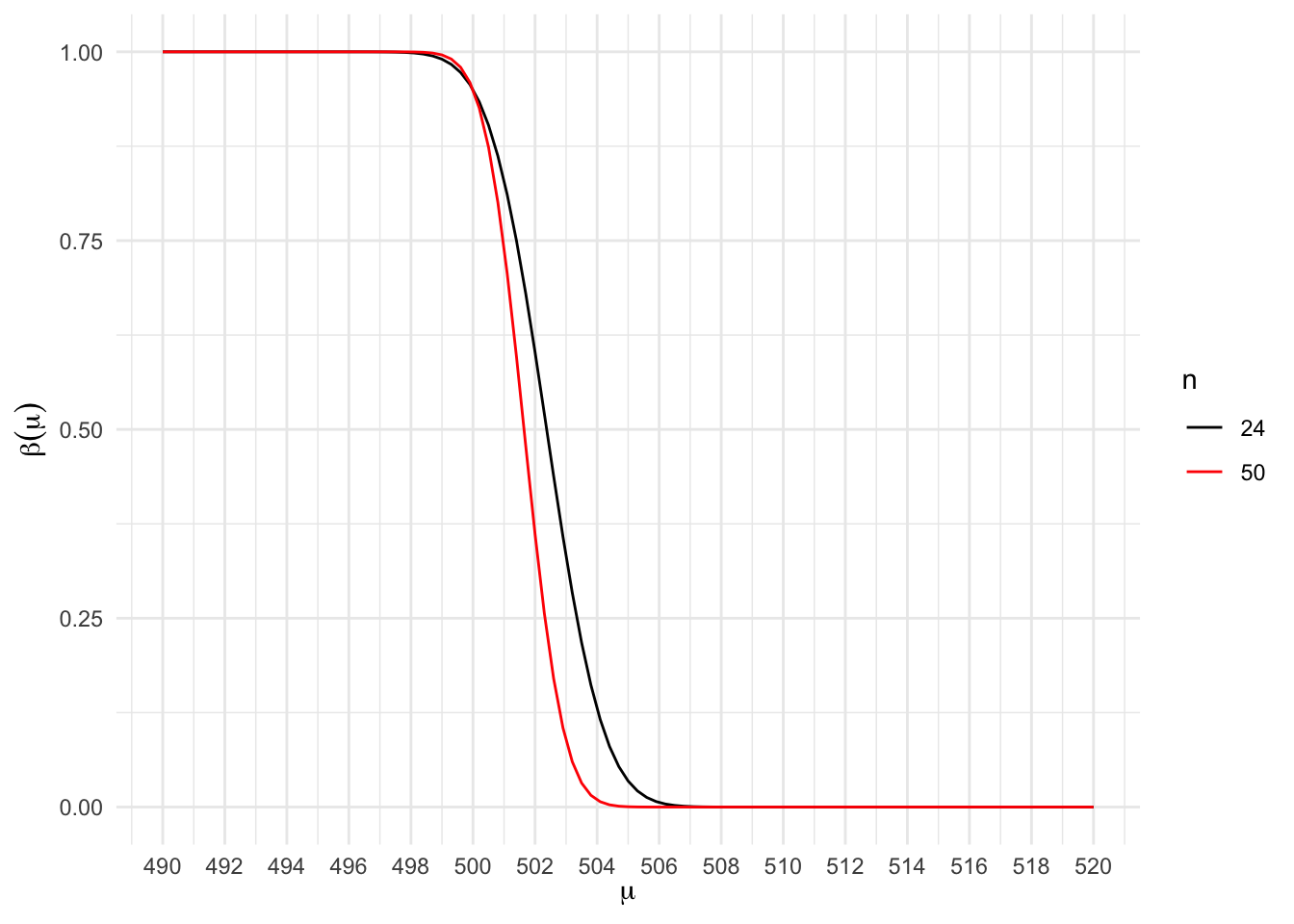

O que percebemos ao analisar o gráfico acima, é que a probabilidade de cometermos o erro tipo II é influenciada pelo tamanho da amostra, de modo que para amostras maiores o erro tipo II tende a decair mais rapidamente para 0. O teste com um tamanho de amostra maior tem menor probabilidade de dizer que a média é 500 quando ela for maior do que 500.

15.2 Poder do teste para um teste unilateral à direita.

Suponha que continuamos avaliando o mesmo cenário (teste unilateral à direita para a média de uma população normal com variância conhecida).

Uma função do erro tipo II bastante útil para a avaliação de um determinado teste de hipóteses é o poder do teste. Ele é obtido como o complementar do erro tipo II, no caso no qual estamos avaliando o poder seria dado por

\[\begin{eqnarray} \pi(\mu) & = & P(\mbox{Rejeitar } H_0| H_0 \mbox{ é falsa}) \\ & = & 1 - P(\mbox{Não Rejeitar } H_0| \mu) \\ & = & 1 - \beta(\mu) \\ \end{eqnarray}\]

Veja que ao contrário do erro tipo II, o poder do teste é uma probabilidade de acerto, logo estamos interessados em calcular qual a probabilidade do teste rejeitar a hipótese nula (falar que a média é maior do que \(\mu_0\)) quando de fato é é maior do que \(\mu_0\). O poder é o complementar do erro tipo II.

Vamos criar uma função que calcula o poder de um teste unilateral à direita.

#Criando a função poder do teste para um teste unilateral à direita 
#do teste de média com variância conhecida
poder_unid = function(n,alfa,mu,mu0,sigma2){
  k = qnorm(p = alfa,
            mean = mu0,
            sd = sqrt(sigma2/n),
            lower.tail = FALSE)
  poder = 1 - pnorm(q = k, 
                    mean = mu, 
                    sd = sqrt(sigma2/n))
  return(poder)
}

Suponha que foi observada uma amostra de 24 valores, qual será o poder do teste se \(\mu =\) 504?

#Calculando o poder do teste se mu = 504
poder_unid(n = 24,
           alfa = 0.05, 
           mu = 504,
           mu0 = 500,
           sigma2 = 50)

[1] 0.8700077

Notamos que a probabilidade de afirmarmos que a média é superior a 500 quando na verdade ela é 504 é de aproximadamente 87%.

Como podemos obter esta probabilidade para diversos valores de \(\mu\), vamos plotar a função criada para valores de \(\mu\) de 490 a 520?

#Plotando a função poder do teste
ggplot(data = tibble(val = c(490,520)), aes(x = val)) +
  stat_function(fun = poder_unid,
                args = list(n = 24,
                            alfa = 0.05,
                            mu0 = 500,
                            sigma2 = 50)) +
  xlab(expression(mu)) +
  ylab(expression(pi(mu))) +
  theme_minimal() +
  scale_x_continuous(breaks = seq(490, 520, 2))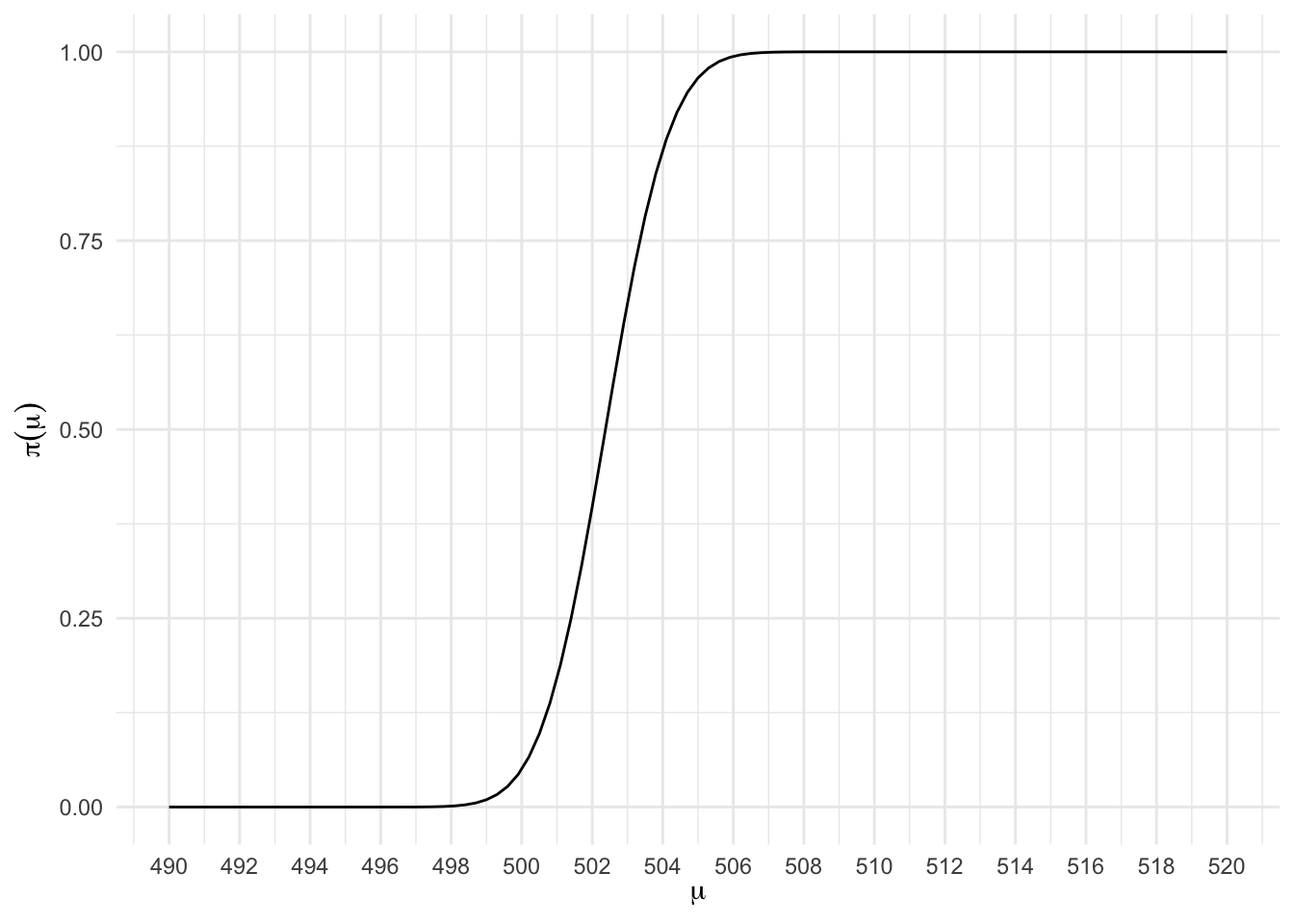

Percebemos que quanto maior for o valor de \(\mu\), maior é a probabilidade do teste dizer que a média é superior a 500. Mais do que isso, percebemos que esta probabilidade cresce rapidamente para 1, um comportamento desejado da função poder.

Abaixo vamos calcular a probabilidade de rejeitarmos \(H_0\), ou seja, afirmar que a média é maior do que 500, quando na verdade ela é 500.

#Calculando o poder do teste se mu = 500
poder_unid(n = 24,
           alfa = 0.05,
           mu = 500,
           mu0 = 500,
           sigma2 = 50)

[1] 0.05

O resultado, como esperado, é o erro tipo I que foi definido para o teste, neste caso 0,05.

Como a função poder é o complementar da função do erro tipo II, o tamanho da amostra também influencia o poder, de modo que amostras maiores terão poderes convergindo para 1 mais rapidamente.

15.3 Desafio

Crie uma função que calcula o erro tipo II para um teste unilateral a esquerda para a média de uma população normal com variância conhecida. Aplique a função para \(n = 30\), \(\alpha = 0,01\), \(\mu = 103\), \(\mu_0 = 100\) e \(\sigma^2 = 40\). Interprete o resultado obtido.
Crie uma função que calcula o erro tipo II para um teste bilateral para a média de uma população normal com variância conhecida. \(n = 30\), \(\alpha = 0,01\), \(\mu = 97\), \(\mu_0 = 100\) e \(\sigma^2 = 40\). Interprete o resultado obtido.
Crie uma função que calcula o poder para um teste unilateral a esquerda para a média de uma população normal com variância conhecida. \(n = 30\), \(\alpha = 0,01\), \(\mu = 103\), \(\mu_0 = 100\) e \(\sigma^2 = 40\). Interprete o resultado obtido.
Plote a função criado no item (1) para valores de \(95 \leq \mu \leq 110\). Para os demais valores necessários, utilizem os mesmos fornecidos na questão.
Plote a função criado no item (2) para valores de \(90 \leq \mu \leq 110\). Para os demais valores necessários, utilizem os mesmos fornecidos na questão.